方程式の近似解
さて、今まで二節を使って「再帰の練習」をしてきました。いや、事実上これらは「再帰の練習」がトピックだったのです。(そして、その再帰ネタを「反復で行う」と言うネタです)
元々、このテキストの背後にあるネタを整理してみると、
- テキスト後半の著者である菅原昭博・現玉川大学工学部電子工学科准教授は東工大出身である。
- 東工大出身である以上、設計理論上、再帰方程式使いまくりの関数型プログラミング言語、Lispに精通している。
- プログラミング未経験の学生に数値計算を迅速に教えるのはLispが最適である。
- しかしながら、90年代初頭のパソコンでは非力過ぎてLispは動かなかった。
- しょーがないので、Lispで扱うネタを当時それなりに流行っていたPascalを模した「擬似プログラム」で解説するしか無かった。
- だから解説がワヤクチャである。
と言う事です。実際、これまでの2節の内容は、Lisp/Schemeの教科書の「最初にやるネタ」としては良くあるトピックなんです。
(一方、当然ながら、このテのトピックは「Pascalの入門書」とか「Cの入門書」には出てきません)
プログラミングは難しい?確かに難しいかもしれません。
しかし、このテの数値計算が「余計難しく見える」最大の理由は、
初心者にとって、「数学的アルゴリズムが難しい」のか、「プログラミング自体が難しい」のか判断が付かない
からなんです。難しい×難しい、だと混乱して当たりまえ、なんですよ。
ですから、通常、「数値計算」ってトピックは「一通りPascal(あるいはC言語)を扱えるようになってから」別の教科書で学ぶ、となってるんです。
そこで当然方策としては「数学的アルゴリズムが難しい」から「プログラミング自体が難しい」を切り離してしまった方が良い、って事になります。単純に「簡単なプログラミング言語を使えば問題の半分は解決する」と言う方法です。
これは成功した、と思います。Python、Ruby等の「動く擬似コード」の導入によって「数学的アルゴリズムが難しい」、だけを意図的に切り離したんです。
今まで、演習問題の回答例を見ていて
「本体がたった2〜3行程度、でプログラムと呼べるのか?」
とか思った人もいるかもしれません。が、実は「2〜3行程度でも」れっきとした「プログラム」です。
と言うか、プログラムは「短く書ければ書けるほど良い」んです。そして、プログラミング言語自体が強力になればなるほど「短く記述する事が」可能になるのです。
これが90年代初頭と今現在の「テクノロジーの差」なのは言うまでもありません。
Python、Ruby、Rはどれも「新しい」言語です(例外はSchemeだけ、なんですが、そもそも背景が数学である以上「古くは」なりません)。プログラミング言語の選択も、原則的には「なるべく新しい言語を選んだ方が良い」と言う事です。
これはテクノロジー選択の原則で、例えば今手元に10万円程度あるとして、何か録画機器を買いたい、とします。ビデオテープレコーダー、DVDデコーダー、ハードディスクレコーダーとあった場合、まあ、十中八九「ハードディスクレコーダー」を買う人が多いでしょう。何故なら「新しいから」ですよね。今更ビデオデッキを買おう、って人はあんまりいないでしょう。何故なら、テクノロジーは基本的には「新しい方が良い」からなんです。プログラミング言語もテクノロジーの範疇である以上、同様の文脈となります。
ここで始めてPython、Rubyなんかのプログラミング言語の存在を知った人も多いと思いますが、プロの現場でも愛用されている、と言うのは先ほど書いた通り「記述能力が高い=短くコードを書けるから」なんです。短ければ短い程「間違い」が混入する確率も低くなりませす。そして、この二つは「Webアプリケーション記述」が特に得意な分野なんで、実は知らないうちに「Python/Rubyで書かれたサイト」を見ている可能性もあります。つまり、あなた方が考えている程「マイナー言語」ではないのです。
また、Rは実際「統計解析の分野」で良く使われているソフトウェアなんで、ここでも「記述が長いと」日常的に使うのがかったるくなるんで、やっぱりなるべくシンプルに書けるように設計されています。これも特殊分野ですが、その分野ではやはり「メジャー言語」なのです。
これらの言語の隆盛は、一つ、コンピュータの処理能力が劇的に上昇した事に由来しています。これらも一昔前だったらマトモに動かすのが大変だったでしょう。しかし、今の標準的なコンピュータだと、CPUの演算速度は最低でも1GHz突破してるでしょうし、メモリにしても1Gb近くは搭載しているケースが多いと思います。既に昔の大型コンピュータの能力を凌駕してるんで、こう言う「記述が短く簡単なプログラミング言語」が登場してきたのです。
ちょっと長くなりますが、大事な事が示唆されている文書があるんで引用してみます。
100年後にコンピュータが何で作られていようが、現在のものより遥かに速いと考えるのは安全な予測だろう。ムーアの法則がこのまま続けば、コンピュータは現在の 7400京倍(73,786,976,294,838,206,464)の速度を得ることになる。想像し難い数字だ。実際、速度の面ではムーアの法則は破れるだろうと考える方が無難な予想だ。18ヵ月毎に2倍になるなんてものは、それが何であれ、いずれ根本的な限界に達しそうだと考えられる。そうだとしても、コンピュータが現在のものよりずっとずっと速くなると考えて良いだろう。たとえそれがたかだか100万倍であったとしても、プログラミング言語の基本的な法則を大きく変えるには十分だ。その中には、例えば現在では遅いと考えられている言語、つまり効率的なコードを生成しない言語の活躍の余地が大きくなるということが挙げられる。
もちろん、依然として速度を要求するアプリケーションもあるだろう。コンピュータを使って解きたいと思う問題のいくつかは、コンピュータ自身によって作られる。例えば、コンピュータで生成されたビデオイメージの処理は、生成側のコンピュータの速度に追い付いていなければならないだろう。さらに、いくらマシンサイクルがあっても本質的にそれを喰い潰してしまう類の処理というのがある。イメージレンダリング、暗号、シミュレーションといったものだ。
いくつかのアプリケーションはますます非効率になって行く一方で、ハードウェアの限界までの速度を要求するアプリケーションがあるとすると、速い計算機を手にするということは、言語は効率においてより広い範囲をカバーしなければならなくなるということだ。既にそれは起こりつつある。人気のある新しい言語の現在の実装は、10年前の基準では驚異的に非効率だ。
これはプログラミング言語だけに起こっていることではない。一般的な歴史の流れだ。技術が進むにつれ、各世代はその前の世代だったらもったいないと思っていたようなことを平気で出来るようになる。30年前の人は、我々がこんなに気軽に長距離電話をかけるのに驚愕するだろう。100年前の人は、ボストンからニューヨークまで翌日配達便で荷物を送るのに、メンフィスを経由すると聞いてひっくり返るだろう。
次の100年の間に、速いハードウェアによって我々が得る余分なマシンサイクルがどう使われるかを当ててみようか。そのほとんどは無駄に使われることになる。
私は、コンピュータの力が貴重であった時代にプログラミングを学んだ。 4KバイトメモリのTRS-80に載せるために、Basicプログラムから全ての空白を抜いたことを覚えている。同じ作業を何度も何度も繰り返すのにマシンサイクルを喰いつづける、おそろしく非効率なソフトウェアのことを考えるのと気分が悪くなる。だが、ここでは私の直観は間違っているんだろう。貧乏が身についてしまうと、例えば医者にかかるといった重要なことに金を使うのを躊躇してしまうようなものだ。
ここでは、マシンが速くなればなるほど工学的な意味での「効率的なプログラミング言語」より「非効率な」しかし「記述能力が高い言語」の重要性が増してくる、と言う事が語られています。つまり、遅いマシンだと「機械に気を遣って」人間側が機械により近い立場の言語を使って「効率的な」プログラムを書かなければならないのですが、今みたいに(また将来的に)マシンが十分な速さを持つと、その重要度の比率は逆転してくる。現代の状況では「記述力の高い言語」を扱うのには十分だ、と言う事が出来るんです。
通大のテキストのように「90年代の常識で」「数値計算を語る」プログラミングの教科書の存在、ってのは本当に害悪なのです。しかも相手は「数学教員免許取得希望者」であって「情報工学専攻」じゃない。少なくともPython、Ruby等の「現存するプログラミング言語のうち、最も簡単な言語」さえそれなりに扱えれば十分、です(もちろん、これさえ扱えない、となればそもそも教員免許取得の能力が無い、のと同義でしょう)。
まあ、別にストイックに「C言語等で効率的なコードをガリガリ書くのも重要」ってのは否定しませんが、今の時代だとそれは「情報工学専門」向けです。そう言うメンド臭さは、繰り返しますが、「数学教員として」必ずしも求められているもの、とは違うのです。
(ホント、さっさとテキスト改訂するべきです)
と言う辺りで前フリを終わっておいて、この節からは本格的な「数値計算」が始まります。
今、僕等の手の中にはPython、Ruby、Scheme、Rと言った動的型付け言語のうちのどれかがあります。そして「再帰」と言う武器もあります。従って、現時点では「プログラミングの面倒なお約束」は「数値計算」自体のトピックとは完全に切り離された状態です。
通大のテキストも「数学的背景」の説明が前半、実装に付いてのアイディアが後半、と完全に切り離されていますね。これは非常にやりやすい、です。
前半の「数学的説明」は「その通り」なんで、それはキチンと読んで理解して下さい。ここは「プログラミング」ではなくって単なる「数学」です。重要な部分は下線を引いていきます。それが後半で「実装する」際のヒントとなるでしょう。
では、始めます。
関数が$f(x)=x^2+2x+1$のような場合は、方程式$f(x)=0$を代数的に解くことができますから、あえてコンピュータを用いてその解を計算する必要はありません。しかし、このように容易に解を求めることができる方程式ばかりではありません。現実には解の存在は分かっているのですが、それをきちんと求めることができない方程式に出会うことのほうが多いのです。ここでは、そのような方程式に対していかなる方法で、その解を見つけるか考えてみましょう。
次にその解決策を2通り説明します。
- 2分法
解析学の基礎を学んでいると、次の連続関数に対する重要な定理が必ず出てきます。
[定理] 関数f(・)は閉区間[a, b]において連続とする。f(a)、f(b)が異符号ならば、方程式f(x)=0は開区間(a, b)において少なくとも一つの解を持つ。
これは有名な「中間値の定理」の一つの系です。また、これが証明されれば「中間値の定理」はこの定理の系として証明されます。
この定理の証明の仕方はいくつかありますが、その中に解を具体的な手順によって求めていくものがあります。
(証明) まず、f(a)<0、f(b)>0の場合に証明しましょう。いま、a0=a、b0=bとおき、m0=(a0+b0)/2を求めます。ここで、f(m0)=0ならば、このm0が求める方程式の解となります。それ以外の場合、
f(m0)>0ならば、a1=a、b1=m0
f(m0)<0ならば、a1=m0、b1=b
とし、m1=(a1+b1)/2を求めます。このとき、f(m1)=0であればm1が求める解となり、そうでないときは、
f(m1)>0ならば、a2=a1、b2=m1
f(m1)<0ならば、a2=m1、b2=b1
として、m2=(a2+b2)/2を求めます。この操作を有限回繰り返して、f(mk)=0となるmkが得られば定理は証明されたことになります。そのようなmkが存在しないときは、無限の繰り返しによって、
a=a0≦a1≦a2≦・・・≦b2≦b1≦b0=b
となる、有界な単調列{ak}と{bk}が得られます。このとき、
$b_k−a_k=(b−a)/2^k$
が成立しますから、この2つの数列は同じ極限値cを持つことがわかります。ところで、数列の作り方から
f(ak)・f(bk)<0
となっています。ここで、k→∞とすれば関数の連続性から、f(ak)とf(bk)はf(c)に収束しますから、
f(c)・f(c)≦0
となり、したがってf(c)=0、すなわちcが方程式の解となります。
f(a)>0、f(b)<0のときは、関数−f(・)に、今の手順を適用します。///
この定理の証明の中で使われた方法をもとにして、方程式の近似解を求める手法を2分法と呼びます。その名の通り、最初に与えられた区間の2等分を繰り返し、目的の解に近づいていきます。- ニュートン・ラフソン(Newton-Raphson)法
関数f(x)の導関数f'(x)が分かっている場合は、方程式f(x)=0の解に対して次の定理が成り立ちます。この定理の中の手順による反復計算によって、解を求める方法をニュートン・ラフソン法と呼びます。
[定理] 関数f(x)は、閉区間[a, b]で2回連続微分可能とし、
- f(a)とf(b)は異符号
- a≦x≦bで、常にf'(x)>0またはf'(x)<0
- a≦x≦bで、常にf"(x)≦0またはf"(x)≧0
- 端点aとbで、|f'(x)|が大きくない方をcとしたとき、
|f(c)|≦(b−a)|f'(c)|
を満たすとする。このとき、区間[a, b]の中の任意の点x0から出発して、
xn+1=xn−f(xn)/f'(xn)
により定められた数列{xn}は、方程式f(x)=0の唯一の解に収束する。
この定理で1.の仮定から前の定理を使って開区間(a, b)の間に少なくとも1つ解があり、2.からそれが唯一であることがわかります。3.は関数のグラフがその区間で上に凸であるか、下に凸であるかを示しています。4.の仮定は|f'(x)|が最小になる端点におけるこの関数の接線が区間[a, b]でx軸と交わることを意味します。
(証明) ここでは次の場合について証明します。
f(a)<0、f(b)>0、f'(x)>0、f"(x)≧0、c=a
他に3つの場合が考えられますが、すべてこの場合に帰着されます。
方程式f(x)=0の唯一の解をsとおくことにし、点x0をs≦x0≦bであるとします。(x0, f(x0))における接線
y=f'(x0)(x−x0)+f(x0)
x1=x0−f(x0)/f'(x0)
となり、f'(x0)≧0、f(x0)>0からx0≧x1が成立します。一般に、
x0≧x1≧x2≧・・・≧s
が成り立つことを帰納法で示します。xn≧sならば、平均値の定理より、
f(xn)=f(xn)−f(s)
=(xn−s)f'(γ) (s≦γ≦xn)
となります。ここでf"(x)≧0から、
f(xn)≦(xn−s)f'(xn)
となります。したがって、
xn+1=xn−f(xn)/f'(xn)≧s
が成り立ち、f(xn+1)となります。単調減少であることも。上の式からあきらかです。
下に有界な単調減少列は極限を持ちますから、それをαとすればs≦αとなります。fとf'の連続性から、数列を作り出す式において、n→∞とすれば、
α=α−f(α)/f'(α)
からf(α)=0です。ここで、方程式f(x)=0の解の一意性からα=sとなります。///
以上の2つが、方程式の解を求める方法の数学的基礎となるものです。これを基にして、各方法のプログラムを作成します。- 収束の判定
ところで、上に書かれたことをプログラミングするにあたって一つ問題があります。反復により生成される数列{xn}の収束を一般にどのように扱えばよいのかということです。コンピュータがいくら高速の繰り返しを得意としても、いかなる処理も無限に行うことはできません。コンピュータを使うのは、その高速性を活かして短時間で求める結果が欲しいからです。無限の時間をコンピュータに与える訳にはいきません。
コンピュータによる実数型の計算は、近似計算であることを思い出してください。今のように方程式f(x)=0の解を求める場合、その解を求めるための反復計算や関数の値を計算するときに計算誤差が入り込んできます。そこで、
「あらかじめ許容される誤差εを与えておき目的の解の値がその誤差の範囲内に納まれば、すなわち
|xn−xn+1|<ε
であれば収束したとみなす」
または、
「方程式の解における関数値を計算するときの計算誤差δを、前もって見当をつけておき、
|f(xn)|<δ
となったら収束したものとみなす」
のどちらかの判定基準を用いて反復を終了し、その時点におけるxnを解とするのが一般的です。当然、近似値となります。
[課題3・1] 関数f(・)が与えられているとき、方程式f(x)=0の解を2分法により求めよ。
まず、関数f(x)を計算するサブプログラムはすでにあるものとして、次のようにプログラムを分解します。
- 出発点[a, b]の左端aと右端bを入力する
- 上の区間に2分法を用いてf(x)=0の解を求める
- 解を出力する
1番目の入力では、このaとbが適当なものであるか判断しなくてはなりません。2分法では、出発区間の左端aと右端bにおける関数の値が異符号でなければなりません。それを考慮して、さらに次のように詳細化します。
- 2つの実数a、bを読み込む
- もし、f(a)f(b)>0 ならば プログラム終了
ここで、「f(a)f(b)>0」というのは、f(a)とf(b)は同符号であるかの判定を行うためのものです。共に正であるか共に負であるか別々に調べなくとも、この積の正負だけで必要な判断を行うことができます。
2番目の命令をどのように詳細化するかが問題です。ここで、2分法をもう一度簡単に説明しましょう。
左端akとbkで異符号の関数値を持つ区間[ak, bk]を、その中点mkで2つの区間[ak, mk]と[mk, bk]に分けます。f(mk)≠0ならば、このうち少なくとも一方の区間で、左端と右端の関数値が異符号となります。その区間を[ak+1, bk+1]とします。これを繰り返して得られる無限数列{ak}、{bk}は、共に方程式f(x)=0の解に収束します。
ここでは、前もって与えたεを使って|ak−bk|<εで収束と判定することにします。
いままでの説明から、2分法は次のような手順で実行すればよいことがわかります。ただし、区間[a, b]の中には方程式の解が存在し、変数mはその中点を意味します。また、tは一時変数で次の二つの判断で使われます。最初の判断では、f(a)とf(m)が同符号になりますからmを新たにaとします。次の判断ではf(a)とf(m)が異符号になりますからmを新たにbとします。まず、f(m)=0となることはありませんが、もしそうなった場合でもa=bとなり反復は終了します。
- |a−b|≧εである限り次を繰り返す
{
- m←(a+b)/2
- t←f(a)×f(b)
- もし t≧0 ならば a←m
- もし t≦0 ならば b←m
}
この反復が終了した時点の変数aあるいはbの値を、方程式の解とします。
以上をまとめて、プログラムは次のようになります。ここで、誤差として10-6をとってみました。
- 定数 ε=1.0E-06 : 実数型
- 変数 a、b、m、t : 実数型
{- a、bの値を読み込む
- もし f(a)×f(b)>0 ならばプログラム終了
- |a−b|≧εである限り次を繰り返す
{
- m←(a+b)/2
- t←f(a)×f(m)
- もし t≧0 ならば a←m
- もし t≦0 ならば b←m
}- a (またはb) の値を出力する
}
さて、特にツッコミもなく、ここまで至りました。と言うのも、殆どが「数学の話」ですんで「その通り」としか言いようがないのです。
また、今回は、上の「疑似プログラム」にも敢てツッコんでません。これも後で自分でwhile文で実装してみる、ってのも良い練習だとは思うから、です。
しかしながら、ここでは2分法も「再帰の枠組み」で記述することにします。と言うのもそっちの方が「簡単だから」ですよね。
ところで、上の「疑似プログラム」を見ると、条件節が入れ子になっていて、あまり美しくありません。入れ子が必要になる時はなる、んですが、不必要に入れ子になるとコードの流れを把握するのが一般的には難しくなるから、なんです。
また、下線部引いてきたところと、上の疑似プログラムの流れを見ると、実はおおまかに言うと「次の事が」プログラムの流れになるのです。
- プログラムBisectionMethodの引数はf、a、bの3つとする。→表記は取り合えずここではBM(f, a, b)とする。
- 計算誤差εを$$\epsilon=10^{-6}$$とする。
- 中間点mをm=(a+b)/2とする。
- 条件1:もしf(a)×f(b)≧0だったらプログラムはエラーを返す。
- 条件2:もし|a−b|<εだったらaを返す。
- 条件3:もしf(a)×f(m)>0ならばBM(f, m, b)を呼び出す。←再帰!!!
- 条件4:それ以外の場合、BM(f, a, m)を呼び出す。←再帰!!!
だいぶ圧縮されましたね。再帰は「分岐」ですし、「反復が分岐で書ける」のなら、結果全部分岐なんで入れ子にする必要が全く無い、と言う事なのです。
注釈を少々。
まず、上の疑似コードの大本の1.を見てほしいんですが、通大テキストでは入力値はa、bの二つの実数だったんですが、上の疑似コードではf、a、bと三つに増えています。a、bは同じで良いとしてfとは何だ???
fは「関数」です。つまり、ここでは、適当な関数fを引数として与えて、その解を2分法で解けるようにしよう、としているわけです。
ここで、通大「コンピュータ」テキストのp144辺りを見てほしいんですが、Pascalによる2分法のコード例が書かれています。これ見ていると中にx*x*sin(x)と書かれた部分があるでしょう?
実はこの部分は2分法のロジック自体とは全く関係無い部分だと言う事です。つまり、このコードはx*x*sin(x)と言う関数「だけ」を2分法しようと言ってるんですね。
ちょっと待てよ……って事はx*x*sin(x)と言う関数以外を2分法する場合は?答えはその部分を書き換えて使わないとならないと言う事を示しているのです。
しかもPascalは一般的にはコンパイラ型の言語なので、ソースコードを書き換えては一々コンパイルせねばならない……要するに汎用性としてはイマイチ、なんです。シチメンド臭いですね。
だったら任意の関数を引数に与えて、それを2分法で解いた方が面白いし便利だろ、って事です。従って、ここでは引数fを増やして2分法を「任意の関数f」に適用する事とします。
次に条件3と条件4ですが、これらは通大テキスト「疑似プログラム」繰り返し内のa、ないしはbへのtの代入と同じ行為をしています。「疑似プログラム」では変数への代入だけ、ですが、再帰版では再帰の肝、「今作成している関数自体の引数を変更して呼び出す」スタイルになっています。
Pythonによる2分法
# -*- coding: utf-8 -*-
def BisectionMethod(f, a, b):
eps = 1.0E-06
m = (a + b) / 2.0 # ここに注意
if f(a) * f(b) > 0:
raise ValueError
elif abs(a - b) < eps:
return a
elif f(a) * f(m) > 0:
return BisectionMethod(f, m, b) # ここで再帰
else:
return BisectionMethod(f, a, m) # ここで再帰
再帰部分はまあ、良いですよね。
Pythonのコードでの注意点は
m = (a + b) / 2.0の部分です。ここを決してm = (a + b) / 2と記述してはなりません。と言うのも、Pythonの場合、整数/整数と言う表記をすると解も整数になる、と言う性質があるから、なんです(これは他の言語、例えばC言語なんかにも見られる性質です)。正確に言うと、余りを切り捨てて商だけ返してしまうのです。
そうすると中点が必ず(中途半端な、しかも実際は中点ではない)整数として計算されて、収束計算が終わらず無限ループに突入してしまうのです。それを避ける為には、割る方の数、この場合は2ですが、これを実数型として認識させる為にあえて小数点以下を記述して2.0としなければならないのです(もちろん、与える引数を必ず実数にする、って回避法もあるんですが、メンド臭いでしょう)。
この辺は一回はハマるので気をつけて下さい(僕も良くハマります・笑)。
Rubyによる二分法
def BisectionMethod f, a, b
eps = 1.0E-06
m = (a + b) / 2.0 # ここに注意1
if f[a] * f[b] >= 0 # ここに注意2
raise
elsif (a - b).abs < eps # ここに注意3
a
elsif f[a] * f[m] > 0
BisectionMethod(f, m, b) # ここで再帰
else
BisectionMethod(f, a, m) # ここで再帰
end
end
再帰部分はまあ、良いですよね。
2分法でのRubyのコードでは注意点が全部で3つあります(ちょっと多いですね)。順番に説明していきます。
Rubyのコードでの注意点その1。
m = (a + b) / 2.0の部分です。ここを決してm = (a + b) / 2と記述してはなりません。と言うのも、Rubyの場合、整数/整数と言う表記をすると解も整数になる、と言う性質があるから、なんです(これは他の言語、例えばC言語なんかにも見られる性質です)。正確に言うと、余りを切り捨てて商だけ返してしまうのです。
そうすると中点が必ず(中途半端な、しかも実際は中点ではない)整数として計算されて、収束計算が終わらず無限ループに突入してしまうのです。それを避ける為には、割る方の数、この場合は2ですが、これを実数型として認識させる為にあえて小数点以下を記述して2.0としなければならないのです(もちろん、与える引数を必ず実数にする、って回避法もあるんですが、メンド臭いでしょう)。
この辺は一回はハマるので気をつけて下さい(僕も良くハマります・笑)。
Rubyのコードでの注意点その2。引数に関数fを取る、と言う形にしていますが、コード内部でその関数fを引数aとbや変数mに適用しています。こう言う場合、Rubyでは特殊な書法を採用していて、そう言う場合、
f[a]とかf[b]とかf[m]と記述します。決して数学記法と同様にf(a)とかf(b)とかf(m)とか記述しないように。括弧が違うのです。Rubyでのコードでの注意点その3。Rubyでは絶対値を取るとき特殊な記法を用います。通常、絶対値を取る場合、絶対値を取る関数abs(大体のケースでは、絶対値=absolute valueからこの名前が付いている)は絶対値を取りたい数値、ないしは式の(どんな形であれ)前方に書くんですが、Rubyの場合は
数値/式.absと言う書き方をします。これはかなり変わった書法に見えますが、こう言うのは実はオブジェクト指向型言語と呼ばれる言語では割に良く見かける書き方です。Rubyはオブジェクト指向型言語だ、と言うのをどっか頭の片隅にでも置いておいてください(そして、それはそれでかなり一環しているのがRubyの特徴です)。Schemeによる二分法
(define (BisectionMethod f a b)
(let ((eps 1.0E-06)
(m (/ (+ a b) 2))
)
(cond ((positive? (* (f a) (f b)))
(error a b))
((< (abs (- a b)) eps)
(exact->inexact a)) ;ここに注意
((positive? (* (f a) (f m)))
(BisectionMethod f m b)) ;ここで再帰
(else
(BisectionMethod f a m)) ;ここで再帰
)))
再帰部分はまあ、良いですよね。
Schemeのコードでの注意点は、まあ、注意点、って程ではないんですけど、最後の結果を返す場合、単に
aを返すのではなくってexact->inexactと言う命令を使って浮動小数表記に変換した方が見やすい、と言う事です。と言うのも、Schemeはプログラミング言語としては珍しく分数を扱えます。これは元々、世界の数理科学系大学の頂点と言うべきマサチューセッツ工科大学が「工学上の限界で不正確な値を返すプログラミング言語を好まなかった」と言う事に由来しています。それじゃあ数理科学の授業で(あくまで)数学的理論を説明するのが困難になるから、です。
この事を解決する為に、マサチューセッツ工科大学は「分数で返せる計算は分数で返す」と言うとてつもない暴挙に打って出て、従って、少なくとも表面的には、Schemeの二分法では「分数を使って延々と繰り返し計算を行っている」(!)のです。これは他のプログラミング言語ではあまり見られない(しかも優秀な)特徴です。
従って、単純に
aを返させると分数表記で返してくる、んですね、Schemeは。そこでexact->inexactと言う命令で(意味は正確数から不正確数への変換を表す)一般的な「望まれる」結果に変換しておくわけです。Rによる二分法
BisectionMethod <- function(f, a, b) {
eps = 1.0E-06
m = (a + b) /2
if (f(a) * f(b) > 0) {
return(NA)
}
else if (abs(a - b) < eps) {
return(a)
}
else if (f(a) * f(m) > 0) {
return(BisectionMethod(f, m, b)) #ここで再帰
}
else {
return(BisectionMethod(f, a, m)) #ここで再帰
}
}
再帰部分はまあ、良いですよね。
この中では一番、特に問題が無く「思った通りの」計算結果を返してくれるのがRです。さすが統計解析(数値計算)専門のプログラミング言語だけあって良く出来ています。
無名関数
さて、もう一度繰り返しますが、通大の「コンピュータ」テキストのp.144の例示は、「$f(x)=x^2 sin(x)$と言う関数"だけを"2分法で計算する」プログラムです。万が一、$f(x)=x^2 sin(x)$「以外の」関数に2分法を適用したい場合、一々プログラム本体に埋め込まれたx*x*sin(x)を随時修正して「コンパイルしなおして」結果を見ないとなりません。
これは、あまりにもメンド臭いんで、ここでは「任意の関数fも引数として与えて」計算させるスタイルを取りました。
ここでは、その「引数としての関数fの与え方」を説明しようと思います。これは各言語毎に違います。
その話をする前に、通大テキストで扱われていた$f(x)=x^2 sin(x)$のグラフをちょっと見てみましょうか。
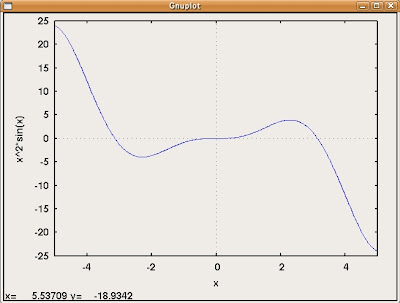
こう言う場合もMaximaは便利ですね。チャッチャとグラフが描けます。また、作った数値計算のプログラムの動作確認をする場合にも、こう言った「既存の」アプリケーションは重宝します。計算結果を照らし合わせる事が出来る。
さて、任意の点a、bを選びましょうか。2分法の論理によると、
- 収束値の中点mはf(x)とx軸が交差している点である。
- f(a)とf(b)は異符号でなければならない。
との事でした。動作確認をする為に逆に考えていくわけですね。
そうすると、グラフを見ると、例えばx=3付近でf(x)はx軸との交点を持っています。そしてその両側のある範囲はどう見ても異符号ですよね。
そこで。キリの良い数字として、a=2、b=4を初期値としましょう。
次に、各プログラムに任意の関数fを与えるんですが、プログラミング言語毎に違う記法があります。
ざーっと紹介しますが、
- Pythonの場合:
lambda 変数: 式 - Rubyの場合:
lambda{|変数| 式} - Schemeの場合:
(lambda (変数) (式)) - Rの場合:
function(変数){式}
と言う形で記述します。これらの記法は「名前の無い関数」と言う意味で、通称無名関数と呼びます(あるいは、R以外はすべてlambdaと書いているのでラムダ式、と言う言い方もします)。
例えば、今は$f(x)=x^2 sin(x)$が対象となる関数なんで、それぞれの言語に合わせた無名関数は
- Pythonの場合:
lambda x: x * x * math.sin(x) - Rubyの場合:
lambda{|x| x * x * Math.sin(x)} - Schemeの場合:
(lambda (x) (* x x (sin x))) - Rの場合:
function(x){x * x * sin(x)}
となります。形式的には$f(x)=x^2 sin(x)$として与えている、と言う事が分かるでしょう。
これで、任意の関数fを引数として与える事が出来るのです。
従って、それぞれのインタプリタ上での入力コマンドは、
- Pythonの場合:
BisectionMethod(lambda x: x * x * math.sin(x), 2, 4) - Rubyの場合:
BisectionMethod(lambda{|x| x * x * Math.sin(x)}, 2, 4) - Schemeの場合:
(BisectionMethod (lambda (x) (* x x (sin x))) 2 4) - Rの場合:
BisectionMethod(function(x){x * x * sin(x)}, 2, 4)
となります(注:Pythonだけは、mathモジュールを明示的に呼び出す必要があるので、インタプリタで上の関数を走らせる前に
import mathと言うコマンドを走らせて下さい)。恐らくどれも結果は、桁数は違いますが、
3.1415920257568359
辺りの値を返してくる、と思います。これは$sin(\pi)=0$から、$f(\pi)=\pi^2 sin(\pi)=0$になるのは容易に想像付きますね。だから円周率π回りの値を返してきたのです。
また、円周率 1,000,000 桁と合わせてみても少数点以下第6桁までは数値があってるのが分かるでしょうか?これは計算誤差εの精度を$10^{-6}$にした事に由来しています。これ以降は「誤差を含む」結果を返してる、と言う事ですね。
これでこれら2分法のプログラムは「上手く動いている」のが分かりました(と言うか、数学的に見て「上手く動く」のは当たり前なんですが・笑)。
他にも様々な無名関数や初期値a、bを与えてみて動作を確認してみて下さい。
ちなみに、質問<3331>なんかはこれがベースの課題ですね。
[課題3・2] 関数f(・)とその導関数f'(・)が与えられているとき、方程式f(・)=0の解をニュートン・ラフソン法により求めよ。
ニュートン・ラフソン法は理論的には2分法と比べて難しいのですがプログラムは逆に作り易くなります。基本部分は前のプログラムと同じですから一気にプログラムを書き上げてしまいましょう。
- 定数 ε=1.0E-06 : 実数型
- 変数 x0、x : 実数型
{- x0の値を読み込む
- x←x0−f(x0)/f'(x0)
- |x−x0|≧εである限り次を繰り返す
{
- x0←x
- x←x0−f(x0)/f'(x0)
}- xの値を出力する
}
ここで、変数x0は前の反復より得られた値を保存しておくためのものです。その値を用いてさらに計算をし、結果を変数xに格納します。xとx0の値が十分近ければ、それは方程式の近似解であるとみなして反復を終了します。
定理の仮定は比較的狭い区間で満たされることが多く、初期値の与え方によってニュートン・ラフソン法で目的の解に収束しないときがあります。実際に使う場合は、2分法を併用したり、おおよそのグラフを書く等の注意が必要です。
<演習問題>
- 手元の電卓で(1÷3)×3を実行し、結果を確認せよ。
- ニュートン法は初期値によって目的の解が得られないときがある。その解をグラフで考えよ。
ええと、ニュートン・ラフソン法ですか。確かに大して難しく見えません。
ところで、ここでのニュートン・ラフソン法は、
関数f(x)の導関数f'(x)が分かっている場合
との事なんで、微分自体をプログラムで行うわけではないと言うトコがミソです。
例えば、通大「コンピュータ」テキストのp.145のPascalでのサンプルプログラム「NewtonRaphson」を見てほしいんですが、ここにもロジックに全く関係がない
f:=x*x - 2の記述やらDf:=2*xの記述やらがありますね。2分法の時でも見たように、ここのプログラムも$f(x)=x^2−2$専用のニュートン・ラフソン法のプログラムになってると言う事です。これも$f\prime(x)=2x$なんで、ちょっと見れば分かるでしょう。従って、微分自体は人手で行わなければダメだ、と言う事です。
もっとも、プログラムでの自動微分は一般に難しい為、これはこれで妥当な戦略だ、とは言えます。
(ここでもMaximaなんかはかなり自由自在に微分/積分を行ってくれているので、如何に優秀なソフトウェアなのか分かるでしょう。数値計算とはまた違う記号処理と言う方法を用いているのですが、一般的にプログラミングはとても難しいです。)
そこで、ここではf(x)と微分係数Df(x)の二つも(無名関数での)引数として与える、と言う事にしてみます。シナリオは以下の通りです。
- ここでは取り合えず、f、Df、x0と言う三つの引数を取るプログラムをNR(f, Df, x0)と呼ぶ。
- 計算誤差εを$$\epsilon=10^{-6}$$とする。
- x=x0−f(x0)/f'(x0)とする。
- もし、|x−x0|<εなら結果としてxを返す。
- そうじゃなかったらNR(f, Df, x)を呼び出す。←再帰!!!
本質的には局所変数x=x0−f(x0)/f'(x0)を設定する必要は無いんですが、プログラム内にxを呼び出すトコが多いんで、こう言う形になっています。要するに一々右辺のx0−f(x0)/f'(x0)を書くのがメンド臭い、と言う建設的な理由に基づいています(笑)。こう言う感じで「良く使う計算式は局所変数にしてしまう」と言うのはアリです。その辺は各自色々工夫してみて下さい。
では実装に入りましょうか。
Pythonによるニュートン・ラフソン法
def NewtonRaphson(f, Df, x0):
eps = 1.0E-06
x = x0 - 1.0 * f(x0)/Df(x0) # ここに注意
if abs(x - x0) < eps:
return x
else:
return NewtonRaphson(f, Df, x) # ここで再帰
再帰はまあ、良いですね(いい加減慣れてきたでしょう・笑)。
Pythonの注意点は
x = x0 - 1.0 * f(x0)/Df(x0) の部分なんですが、決してx = x0 - f(x0)/Df(x0)とは書かない、と言う事です。疑似コードには無い1.0 *を付け忘れちゃいけない。理由は2分法の場合と同じです。Pythonは整数/整数の計算だと整数を返しちゃうから、なのです。
1.0 *を付け足す事によって、結果1.0 * f(x0)は整数ではなくって実数だと認識され、以降の収束計算が滞り無く行われる、と言うわけです(逆に言うと1.0 *が無いと収束計算が上手く行きません)。亀田自身はこれは結構不具合なんじゃないか?とか思います。実際、Pythonの提供元もこれは不具合だ、と認めているようで、将来的にリリースされるPython3.0では改良予定だそうです。少なくとも、「動的型付け言語」で数値の型を色々気にしながらプログラムを打つのはあまり効率的ではない、と僕も思います(しかも明示的に型変換する方法も見当たりませんしね)。
2009年1月30日追記:新しくPython3.0がリリースされている模様です。亀田はまだ確かめていません。
従って、ここで提示されているコード類は既に少々古くなっています。亀田が使用したPythonのヴァージョンはPython 2.5.2です。いまだ配布されている現役のヴァージョンなんで、取り合えずPython2.5.2を使っていて下さい。Python3.0用に記事を書き換えるかどうか、は今のところ未定です。
Rubyによるニュートン・ラフソン法
def NewtonRaphson f, df, x0 # ここに注意1
eps = 1.0E-06
x = x0 - f[x0].to_f / df[x0] # ここに注意2
if (x - x0).abs < eps
x
else
NewtonRaphson(f, df, x) # ここで再帰
end
end
再帰はまあ、良いですね(いい加減慣れてきたでしょう・笑)。
Rubyの注意点その1。疑似コードでは微分係数での引数をDfと表記してますが、Rubyでは引数に大文字は使えないようです。従って、Ruby版では微分係数を表す引数をすべて
dfにしてあります。Rubyの注意点その2。
x = x0 - f[x0].to_f/df[x0] の部分なんですが、決してx = x0 - f[x0]/df[x0]とは書かない、と言う事です。疑似コードには無い.to_fを付け忘れちゃいけない。理由は2分法の場合と同じです。Rubyは整数/整数の計算だと整数を返しちゃうから、なのです。
.to_fを付け足す事によって、明示的にf(x0).to_fは整数ではなくって実数に変換され、以降の収束計算が滞り無く行われる、と言うわけです(逆に言うと.to_fが無いと収束計算が上手く行きません)。Rubyはこのような明示的な型変換のメソッドを持っています。また、この記述法にも一般的なオブジェクト指向言語の影響が見られます。
ちなみに、
.to_fは"to float"、つまり「浮動小数点数(実数)に変換せよ」と言う命令を意味しています。Schemeによるニュートン・ラフソン法
(define (NewtonRaphson f Df x0)
(let ((eps 1.0E-06)
(x (- x0 (/ (f x0) (Df x0))))
)
(if (< (abs (- x x0)) eps)
(exact->inexact x)
(NewtonRaphson f Df x)) ;ここで再帰
))
これは問題無いでしょう。再帰も既に慣れてきたでしょうしね。
Rによるニュートン・ラフソン法
NewtonRaphson <- function(f, Df, x0) {
eps = 1.0E-06
x = x0 - f(x0) / Df(x0)
if (abs(x - x0) < eps) {
return(x)
}
else {
return(NewtonRaphson(f, Df, x)) #ここで再帰
}
}
これも特に問題無いでしょう。再帰も既に慣れてきたでしょうしね。
なお、Rは統計解析/数値計算ソフトなので、ニュートン法を実行するunirootと言う組み込み関数がある事を申し添えておきます。
さて、$x^2-2$の解を考えると$x=\sqrt{2}$、$x=-\sqrt{2}$になる事は分かります。これは非常に確かめやすいですね。
無名関数を利用して、初期値x0を2として各プログラムで解を一つ求めてみましょう。インタプリタに入力するコマンドは以下の通りです。
- Pythonの場合:
NewtonRaphson(lambda x: x * x - 2, lambda x: 2 * x, 2) - Rubyの場合:
NewtonRaphson(lambda{|x| x * x - 2}, lambda{|x| 2 * x}, 2) - Schemeの場合;
(NewtonRaphson (lambda (x) (- (* x x) 2)) (lambda (x) (* 2 x)) 2) - Rの場合:
NewtonRaphson(function(x){x * x - 2}, function(x){2 * x}, 2)
これで計算すると、恐らく初期値2の近傍の解として、桁数は違うでしょうが、次のような数値が得られる事と思います。
1.4142135623746899
これは確かに$\sqrt{2}$に極めて近い値となっています。
また、これも一応、確実な値は小数点以下第6位まで、となっています。それ以降は計算誤差を含んでいるんで、あまり信頼出来ませんね。
他にも関数fと初期値x0を色々と変えてみてニュートン・ラフソン法を試してみて下さい。
<演習問題回答例>
- 省略。
- これはこのページを参考の事。


















