高校数学の窓過去問検索

質問＜３６９０＞２００８／２／２７ from=かもめ 「多角形の内角」

これは、「Yahoo！知恵袋」に投稿されていた質問です。
「現在中３なんですが、正ｎ角形の内角の和は１８０（ｎ−２）°だと習いました。
その式にあてはめると正１００角形、正１０００角形と角の数がたくさんになると
その内角は限りなく１８０°に近づいていくと思います。しかし角の数を増やしていくと
最終的には円という形になっていくと思うのですが、
そもそも内角が１８０°の円の形の図形なんてものはありうるのでしょうか？
また、円の内角は１８０°なんですか？
うまく説明ができませんが、僕を納得さしてください。 」
「内角は１８０°」というのは、ひとつの内角が１８０°と言う意味です。
しかし、質問者が中学生なので、回答者もうまく回答ができなかったようです。
僕も、この質問が気になるので、高校レベルの数学で、解説をお願いします。

★希望★完全解答★



僕もYahoo！知恵袋見ましたが、大変良い回答が集まってると思いますよ。
まあ、あれ以上の回答となれば難しいんじゃないんですか?多分。

問題は、

その式にあてはめると正１００角形、正１０００角形と角の数がたくさんになるとその(一つの)内角は限りなく１８０°に近づいていくと思います。

と言う一文です。これは正しい。間違いありません。
ただし、勘違いしてほしくないのは、「180°に近づいていく」≠「180°である」と言うことです。
確かに、現実的な感覚では「超多角形は円に近づいていくだろうしそんな物体は(技術的に)作れないだろうから、円盤になっちゃうだろうな」と言うのは正しいです。しかしながら「正しい日常感覚は常に数学的感覚を代弁しているワケではない」って事なんですよ。ここを勘違いすればダメなんです。
数学が問題にしているのは、あくまで「数学的抽象性だけ」なのです。

ちょっと別の例を挙げましょう。
良く、面白い例として挙げられるのは物理学の基本的な概念、速度ですね。
速度は微分公式を用いて、位置の変位を、経過時間をtとして次のように「古典力学では」表現されます。



では、ここで、議論をシンプルにする為、変位に着目してみます。一体ここで議論されている微小変位とは一体何なのか?「距離を限りなく小さくしていって」「変位を0に近づけて行って」一体どうなるんでしょうね?
「移動距離(変位)」が微分可能である数学的な大前提は関数が「連続である」と言う事です。
まあ、物体が宇宙戦艦ヤマト



みたいに「ワープして」地点Aから地点Bへいきなり移動する、って事はあり得ないワケですから、「自然と」この関数は「滑らかである」と言う条件を満たしています。
と言うことは数学的操作により微小変化は実際観察できそうに思えるんですが、それがそうは問屋が卸しません。僕等の日常の感覚的視点では「物体が術らかな経路で移動している」ように見えても、経路を拡大していくと、「滑らかな」と言う前提は崩れ去っていくのです。一般的に原子くらいに小さい粒子は「色んなモノにぶつかって」ギザギザに見える経路を辿ります。ちっとも「滑らか」じゃありません。従って微視的観点で滑らかじゃない以上、なんて計算は成り立ちませんし、数学的概念を「そのまま」現実の世界に持ち込んでも上手く行かないって事ですね。
では数学はやっぱり役に立たないし間違っているのか?と言うとこれは愚問になるでしょう。そうじゃなくって、「(僕等が見ている範囲での)現実を数学的抽象力で如何にモデル化してるのか?」と言うのが本当のトコなんです。数学は「説明を上手く展開する為の」道具であって、必ずしも「数学自身が」「全ての現実」を上手く説明するワケではないんです。また、それは数学の目的でも範疇でもありません。
いわば抽象力が数学の本質的な部分であって、あくまで「概念的操作」を提供するツールなのです。上の例も「物理の世界では数学の微分が破綻している」と言うような話ではなくって、「物理でも適所に適した数学を適用しなければならない」だけです。微小世界では「また別の数学を」持ち込めばいい、と言うだけの話なのです。

では元の議題に戻ると、


その式にあてはめると正１００角形、正１０００角形と角の数がたくさんになるとその(一つの)内角は限りなく１８０°に近づいていくと思います。


と言う一文は数学的には



と書き表せます。
上記の式を実際Maximaででも計算してみたら分かりますが、



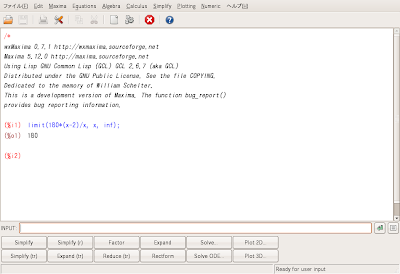
確かに



です。
ただし、上記の式の意味も

nが限りなく大きくなっていくとは180に限りなく近づいていく

と言ってるだけで、

nが限りなく大きくなっていくとは180になる

と言ってるワケではありません。この2つの文(ないしは文意)を混同すればダメだ、と言うことです。前者は数学ですが、後者は「日常感覚的なモノ」であって数学ではありません。

そもそも内角が１８０°の円の形の図形なんてものはありうるのでしょうか？


あり得ません。
まあ、一応円の定義をWikipedia辺りから引っ張ってきますが、そこにはこう書かれています。

数学において、円（えん）とは、平面（2次元ユークリッド空間）上の、ある点 O からの距離が等しい点の集合でできる曲線のことをいう。

角度がどうの、って考える以前に多角形の定義を見ると、

多角形（たかっけい、たかくけい）とは平面上の閉じた単純折れ線、および平面上の閉じた単純折れ線によって囲まれた図形を指す。

ここで

  1. 折れ線とは複数の線分をその端点でつなぎ合わせてできる曲線を言う。

  2. 曲線が単純であるとは、曲線が(端点以外では)自己交差しない事を言う。

  3. 曲線が閉じているとは、長さが有限で端点を持たない事を言う。(厳密にいうと、さらにコンパクトでなければならない)。



と書かれていますね。
ここで、

数学においては、曲線にはその特別な場合として直線や線分の概念を含む。

そうですが、「単純折れ線によって囲まれた図形」である多角形と「ある点 O からの距離が等しい点の集合でできる曲線」である円は定義上折り合いません。多角形が円を含む構図も考えられませんし、逆もまたそうですね。要するに、定義が相反してると言う事です。
いつも言ってますが、数学は定義からスタートするモノであって定義が食い違えば全ての議論は意味が無いのです。ここでも「nが大きくなった多角形は円に限りなく近づいていく」と言うことは出来ますが「円そのものになる」と言う事が定義上あり得ない、って事が分かるでしょう。つまり、数学的な概念上は、例え実作業で作図が難しいにせよ、正1,000角形は正1,000角形ですし、正10，000角形は正10,000角形以外の何者でもないんです。
(ちなみに、Wikipediaで見つけたんですが、理論的にはコンパスと定規だけで、正６５,５３７角形を描けるそうです・笑。当然これは円の作図そのものではありませんね。)

まあ、そんなワケで、むしろ「高校レベルで」と言うのなら、「近づく」はあくまで「近づく」である、って事を理解しておく程度でいいのではないでしょうか?同一視しちゃダメだ、と言う事です。
例えると、いくらIKKOが「綺麗に化粧しても」女性に近づいて行く、とは言えますが、「女性そのものになる事は無い」って事と同じです(違うか・笑)。

以上です。

投稿者 cametan_001 0 コメント

ラベル:

Roots of polynomial(多項式の根を求める)

Maximaでマトモに解けそうにない数式の因数分解を行う場合は[Equation]プルダウンメニューから[Roots of polynomial]を選びます。



この操作により、ジェンキンス・トラウブ(Jenkins-Traub)アルゴリズムと言う数値計算手法によってMaximaは無理矢理多項式の根を求めます。
なお、プルダウンメニューからこのコマンドを選択すると、直前に入力、または出力した数式に対してアルゴリズムを実行しようとします。結果、任意の数式に対して同様の事柄を行うにはコマンドラインでの入力が必要となります。

例題



を因数分解せよ

まずは普通にMaximaの[INPUT:]欄に与式を入力した後、[Enter]キーを打ちます。



その後、[Equation]プルダウンメニューから[Roots of polynomial]を選ぶと根が表示されます。



これにより、与式の根は










の8個の複素数になる事が分かります。
よって、与式の因数分解の近似は



となります。

備考



コマンドラインで数値計算で任意の多項式の根を求める場合は、[INPUT:]欄に

allroots(任意の多項式)

と入力して[Enter]キーを打ちます。
ないしは出力番号を利用して、

allroots(出力番号)

としても実行出来ます。




Maxima Manual: 方程式

投稿者 cametan_001 0 コメント

ラベル:

質問＜３６８１＞２００８／２／６

次のプログラムをBASICで書きたいと思うのですが、
　問）配列にn個の値、,,…,が与えられているとき、このｎ個
　の値の最小値を求めるプログラムを作成する
　どのように作ったらよいのでしょうか？
　どなたかご教授よろしくお願いします

★希望★完全解答★


BASICでどう書くかは知りませんが、原則的に一番単純なアルゴリズムは以下のようなものです。
配列,,…,をと表現した時、

  1. 変数xに配列の先頭を格納し、残りの配列をとする。

  2. プログラム上は、xと配列Aに対して考える。

  3. 配列が空の時、変数xが解となる。

  4. それ以外の時、配列の先頭を取り出し次の繰り返しを行う。

    1. の時、とし、2番に戻る。

    2. の時、新しくとし、として2番に戻る



これで配列内の最小値を探せます。

以上です。



では、いつも通り、BASICの課題をSchemeで解題します。
ちなみに、Schemeにはminと言う関数があって、これで数値の最小値を返してくれるんですね。
書式は以下の通り。


(min ＜任意の個数の数字＞)


例えば、3、8、7、6、5、2、9と言う7個の数字があった場合、


(min 3 8 7 6 5 2 9)


とインタプリタに記入すれば結果を返してくれます。



まあ、これは簡単です。
ただし、これでは題意を満たしません。上の計算結果はあくまで「一番小さい数値」を返しているだけで、「配列内の数値ではない」と言うのがミソなんです。
では、配列(Schemeではリスト)内での数値を対象にするにはどうすればいいのでしょうか?
例えばSchemeでは次のように打ってもエラーを返してきます。



(min '(3 8 7 6 5 2 9))







min: expects argument of type ＜real number＞; given (3 8 7 6 5 2 9)
訳:関数minにリスト(3 8 7 6 5 2 9)が与えられていますが、引数は実数じゃないといけません。

とまあ、minの引数は必ず普通の「数」じゃなくてはいけないのです。リスト(配列)じゃマズい。

こんな感じでリストに並べられた数値から最小値を直接返す組み込み関数はSchemeにも存在しないんですが、問題のような質問を見たら、Scheme使ってる人は十中八九次のように高階関数applyを利用して結果を返すと思います。



(apply min '(3 8 7 6 5 2 9))





これだと上手く計算してくれます。
ここで高階関数applyとは、


(apply ＜関数＞ ＜リスト＞)


と言う書式で記述して、＜関数＞を＜リスト＞に適用する作用があります。上の場合はminと言う関数を与えられたリストに適用してるんですね。
リストの最小値を求める関数を使いまわししたい、と言う場合には、次のように新しく関数を定義すれば題意を満たします。



(define (min_of_list ls)
        (apply min ls))



たった二行で終了、ですね(笑)。恐らくScheme使ってる人はこれ以上複雑な事を考えないと思います(笑)。
ただし、以前にも書きましたが、通常のプログラミング言語の場合、高階関数と言う便利な機能はまだまだ実装していないケースが多いのです。よって、一応、本編のような擬似コードをSchemeで書いてみましょう。



(define (min_of_list ls)    ;関数min_of_listを引数lsとして定義
  (let loop ((x (car ls))    ;lsの先頭をxとする
             (ls0 (cdr ls))) ;lsの残りをls0とする
    (if (null? ls0)          ;ls0が空だったら?
        x                    ;xを返す
        (loop (if (<= x (car ls0)) ;xがls0の先頭以下だったら? 
                  x          ;xのまま
                  (car ls0)) ;じゃなかったらls0の先頭とする
              (cdr ls0)))))  ;ls0の残りとする



こんな感じになります。
これも再帰的定義(BASICで言うとDO〜LOOP構文)を使い、ワンパターンで名前付きlet構文で書いたモノです。
局所関数loopを定義して、その第一引数であるxを条件によって書き換えていく、と言う形式ですね(第二引数は条件によらず、書き換わっていく)。
まあ、構造的にはそんなに難しくないので、BASICに訳する事もそんなに難しくはないでしょう。

投稿者 cametan_001 0 コメント

ラベル: ,

登録: 投稿 (Atom)