高校数学の窓LaTeX版: 質問＜３６８９＞２００８／２／２６ from=guricha 「確率分布、分布関数」

ｒ．ｖ．Ｘの確率分布が、

$P(X=k)=\frac{\left( \begin{array} n \\ k \end{array} \right)\left( \begin{array} n \\ m-k \end{array} \right)}{ \left( \begin{array} n \\ m \end{array} \right) }$ $\dots$ $\left{ \begin{array} 0 \le k \le m \\ 1 \le m < n \end{array}$

であるとき

$\sum_{k=0}^m P(X=k)=1$ をしめせ。

ｎ＝４，ｍ＝２であるとき、Ｘの分布関数Ｆ（ｘ）をもとめ、グラフをかけ。

自分では、
ｋ＝０のとき、 $P(X=0)=\frac{\left( \begin{array} n \\ 0 \end{array} \right) \left( \begin{array} n \\ m-0 \end{array} \right)}{\left( \begin{array} n \\ m \end{array} \right)}=\frac{\left( \begin{array} n \\ m \end{array} \right)}{\left( \begin{array} n \\ m \end{array} \right)}=1$
となってしまい、行き詰まってしまいました。
2.についても、 $P(X=k)=\frac{\left( \begin{array} 4 \\ k \end{array} \right)\left( \begin{array} 4 \\ 2-k \end{array} \right)}{\left( \begin{array} 4 \\ 2 \end{array} \right)}$ となり、

ｋ＝０のとき、 $P(X=0)=1$

ｋ＝１のとき、 $P(X=1)=\frac{16}{6}$

ｋ＝２のとき、 $P(X=2)=1$

このへんで何か根本的におかしいと思い始めました。
アドバイスをお願いいたします。

★希望★完全解答★

お便り２００８／２／２８
from=亀田馬志

＞このへんで何か根本的におかしいと思い始めました。

まあ、おかしいでしょうね。僕もそう思います。

恐らく超幾何分布絡みの問題だと思いますが、
参照ページにある通り、通常分子のnの項は添字が付いていて、
それで初めて確率分布の条件を満たせます。

つまり、問題のコピーミスなのでは、と思いますよ。
参照ページの定義に従うなら解けるとは思います。

お便り２００８／３／１１
from=guricha

早速の解答、ありがとうございます。
参照ぺージを見てとてもよくわかりました。
しかし、やはり問題文の「分子のnの項」には添え字などはなく、
すべて「n」になっていますので、やはり問題のミスのようです。

もし、参照ページの定義にしたがっているとすると、

$\sum_{k=0}^m P(X=k)=1$ をしめせ。

はどのように考えればよろしいでしょうか。

　（追）参照ページの $\left( \begin{array} N_p \\ n-x \end{array} \right)$ は、 $\left( \begin{array} N_q \\ n-x \end{array} \right)$ ということでしょうか？

まず最初に。

　（追）参照ページの $\left( \begin{array} N_p \\ n-x \end{array} \right)$ は、 $\left( \begin{array} N_q \\ n-x \end{array} \right)$ ということでしょうか？

その通りですね。群馬大学の青木先生のページのここは明らかに記述ミスです。掲示板でも使って連絡した方が良いでしょう。
まあ、「数式を間違って覚えている」ワケでは当然なくって、単にタイプミスだと思います。かように、HTMLやらLaTeXで数式打つのはミスを誘発する可能性があります。もうホント打つの大変なんすから(故・林家三平調・謎)。

さて、まず言っておかなければならない事があります。
この問題は、恐らく「間違ってる」だけじゃなくって「非常に記述が曖昧である」と言うことが言えます。
冒頭の、

ｒ．ｖ．Ｘの確率分布

ってのが何の事だかチンプンカンプンです。
仮に、問題が超幾何分布絡みだとしても、それが扱う確率変数はたった一つで、問題の記述に従うと、これはX以外ありません。つまり、rとかvとかは何の事だかちっとも分からないのです。
非常におかしな問題です。
まあ、その辺を心に留めておいてください。

では、問題を

Ｘの確率分布が、

$P(X=k)=\frac{\left( \begin{array} q \\ k \end{array} \right) \left( \begin{array} n-q \\ m-k \end{array} \right) }{ \left( \begin{array} n \\ m \end{array} \right) }$ $\dots$ $\left{ \begin{array} 0 \le k \le m \\ 1 \le m < q \end{array}$

であるとき

$\sum_{k=0}^m P(X=k)=1$ をしめせ。

と読み替えてみます。
ところで、一般に、確率分布P(X)とは全てのkに於いて、

$f(k)=\sum_k P(k) =1$

と言う性質があります。と言うか、任意のP(X)が上の性質を満たす時、P(X)を確率分布と呼んで構わない、と言う事です。ある種、定義なんですね。
つまり、超幾何分布と呼んでる以上、問題の

$\sum_{k=0}^m P(X=k)=1$

ってのは当たり前で、いわば最初から答えが分かっている、と言う事です。
そして、確率分布P(x)に対して、

$f(m)=\sum_k^m P(k)$

と言う関数を特に累積分布関数、または単に分布関数、と呼びます。
まずはここまでが前提知識なんですが、一方、超幾何分布

$P(X=k)=\frac{\left( \begin{array} q \\ k \end{array} \right) \left( \begin{array} n-q \\ m-k \end{array} \right) }{ \left( \begin{array} n \\ m \end{array} \right) }$

に対しての累積分布関数、

$f(m)=\sum_{k=0}^m \frac{ \left( \begin{array} q \\ k \end{array} \right) \left( \begin{array} n-q \\ m-k \end{array} \right) }{ \left( \begin{array} n \\ m \end{array} \right) }$

ってのは形式上は上の通りなんですが、具体的に上の式を整理した形がどんなモノなんだかちっとも分かりません。
困ったことに、少なくともネット検索したり、ないしは亀田が持ってる統計関係の教科書見ても「超幾何分布の累積分布関数」なんてのは見つからなかったです。最初に具体的な式さえ分かってたら計算する必要もないワケですし(笑)、手を抜けます(笑)。宿題だったら書き写しちまえばイッチョ上がり、です。が、そう簡単には行きません(笑)。

さて、困った。
が、問題を良く読んでほしいのですが、

$\sum_{k=0}^m P(X=k)=1$ をしめせ。

と書いていますね。「求めよ」じゃなくって「しめせ」です。微妙な言い回しの違いですが、数学に於いては意味が決定的に違うんです。
つまり、問題としては「具体的な式の形は求めなくて良い」と言う事を暗に言ってるんです。単にどんな形であれ「1になる事さえ分かれば良い」と言ってるのです。分かりますかね?
こう言う「もったいぶった言い回し」の場合は・・・・・・。そうですね、結果が初めっから分かっている以上、数学的帰納法を使って証明してしまえば良いと言う事です。これが方針となります。
しかしながら、実はこの数学的帰納法による証明は、少なくとも亀田がやった以上、何て事なかったです。そんなに難しくなかった。呆気に取られるくらい簡単に終了します。
ではやっていってみましょう。

m=1の時、
で確かに正しい。

m=Nの時、

$\sum_{k=0}^N \frac{ \left( \begin{array} q \\ k \end{array} \right) \left( \begin{array} n-q \\ N-k \end{array} \right) }{ \left( \begin{array} n \\ N \end{array} \right) }=1$

が正しいとすると、

m=N+1の時、

$\sum_{k=0}^{N+1} \frac{\left( \begin{array} q \\ k \end{array} \right)\left( \begin{array} n-q \\ (N+1)-k \end{array} \right)}{ \left( \begin{array} n \\ N+1 \end{array} \right) }$

はN+1=Mと置くと、

$\sum_{k=0}^M \frac{ \left( \begin{array} q \\ k \end{array} \right) \left( \begin{array} n-q \\ M-k \end{array} \right) }{ \left( \begin{array} n \\ M \end{array} \right) }$

と書き換えられて、形式的にはm=Nの時の

$\sum_{k=0}^N \frac{ \left( \begin{array} q \\ k \end{array} \right) \left( \begin{array} n-q \\ N-k \end{array} \right) }{ \left( \begin{array} n \\ N \end{array} \right) }$

と全く同じである。
従って、

$\sum_{k=0}^{N+1} \frac{ \left( \begin{array} q \\ k \end{array} \right) \left( \begin{array} n-q \\ N+1-k\end{array} \right) }{ \left( \begin{array} n \\ N+1 \end{array} \right) } = 1$

となり、題意は数学的帰納法により証明される。

以上です。

なお、2番目の問題に対しての注釈です。
いや、注釈、って程でも無いですが、ちょっとしたTipsを。

特に統計関係に関してなんですが、数学的には怪しい体系を持ってるクセに「計算だけは複雑だ」と言うのが、統計のアタマに来るトコです。
確かに手計算で勉強するのもいいのですが、グラフだ何だを描画したり、試しに色々計算してみる、と言うのはハッキリ言っちゃってパソコンのソフトウェア使ってやった方が速いです。そう言うパソコンを使った「イメージトレーニング」を積んだ方が、純粋数学はさておき、統計関係の場合はマシ、です。
何故なら、「理論の流れを追う」事が計算の複雑さのせいでかなり困難なんですよ。昔っから「数学者(だけじゃないですが)泣かせ」ってのがこのジャンルのアタマに来るトコなんです。何せ相手は「膨大なデータ」だったりするワケですから、たかだか10個以下程度の「データ」相手に計算練習したって、実用的にどうなるモンでもありません。いや、これホントです(笑)。
まあ、その点、現代は「コンピュータ」があるんで、こう言う勉強はコンピュータに頼った方が良いのです。いい時代になりましたね(笑)。
「数学の勉強にコンピュータ使うなんて……」とか抵抗ある人が多いのも分かりますが、だったらそもそもネットで質問しよう、ってのが大間違いですし(笑)、加えて言うなら統計学は数学じゃないです(笑)。だから安心して下さい(笑)。

さて、「統計で使う」とは言ってもMicrosoft Excelはあまり適しません。かなりの確率でプログラミングミス(人為的バグ)があります。まあ、表計算ソフトは便利ではあるんですが、表計算ソフトは所詮表計算ソフト、なんですね。家計簿つけたり顧客管理には向いても「統計解析」には向きません。
以前から、何回かフリーの統計解析ソフトRを紹介していましたが、ここでも改めて統計解析ソフトRを紹介しておきます。
前に＜質問3609＞でも導入指南しておいたんですが、さすがに記事が長いので(笑)、ここに必要な部分だけ転載して加筆しておきます。何か確率/統計関係で悩んだらまずはRに頼ってみてください。

統計解析ソフトRのダウンロードとインストール

Rはタダで手に入るオープンソースの統計解析用ソフトウェアです。強力な統計関数とグラフィック関係のデバイスが含まれているので、この機会にダウンロード/インストールしてみましょう。

ダウンロード&インストールの方法:

Windows 版 R のインストール

Mac 版 R のインストール

Linux 版 R のインストール

Debian GNU/Linux (含む Knoppix)の場合 (インターネット経由でオリジナル版をインストールする場合)
註:Ubuntu/Kubuntuもここに含まれます。ただし、KNOPPIX/MathはRをプリインストール済です。

Vine Linux 版インストール

openSUSE10.2 Linux 版インストール

※:Rの最新版は2.6.0です(2007年10月5日現在)。

それぞれのOS用の指示に従ってダウンロード/インストール/初期設定を行ってください。

Rの起動

Windows版の場合はダウンロード/インストールが終わるとデスクトップ上にRのアイコンが出来てる筈なので、それをダブルクリックすればRが立ち上がります。

Linux版の場合は、まずは端末(ターミナル)を起動します。

コマンドプロンプトにただRと大文字で打ち込むだけでRが端末上で起動します。

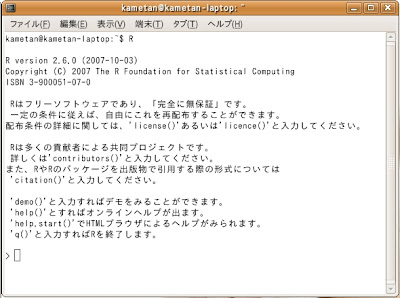
パッケージのインストール

Rの優秀なトコロは、数々の特殊な機能をまとめたプログラム群を追加インストール可能である、と言う部分です。これをパッケージと呼びます。
今回利用するパッケージはRcmdrと言うパッケージです。
Rcmdrと言うパッケージはコマンドラインバリバリのRにマウス操作の為のGUI環境を加える為のモノでこれは結構重宝します。詳しくはこのPDFに書いてあるので、参考にして下さい。マウスだけで基本的なRの操作が出来るようになります。

Windows版Rでのパッケージのインストール方法は、RGui上部にある[パッケージ]プルダウンメニューから[パッケージのインストール...]を選びます。

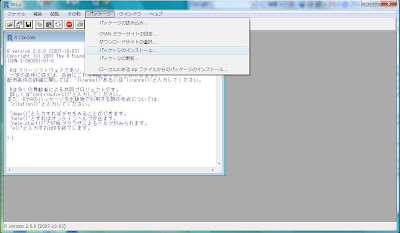
そうしたら、「どこのミラーサイトからダウンロードするのか?」尋ねてくる[CRAN mirror]ポップアップが出て来ます。

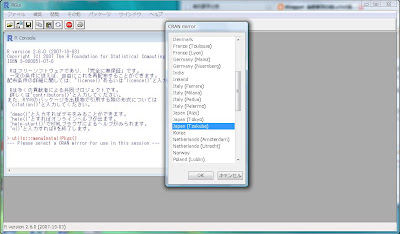
現時点では日本のRのダウンロード先は

福島県:福島県立会津大学 Japan(Aizu)

東京都:国立東京大学 Japan(Tokyo)

茨城県:国立筑波大学 Japan(Tsukuba)

の3箇所となっています。近場の大学のサイトをクリックして[OK]ボタンを押しましょう。

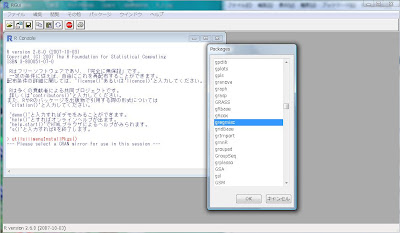
そうすると、インストール可能なパッケージのリスト、[Packages]ポップアップが出てきます。スクロールして、目的のパッケージを探し出してクリック、そして[OK]ボタンを押してください。

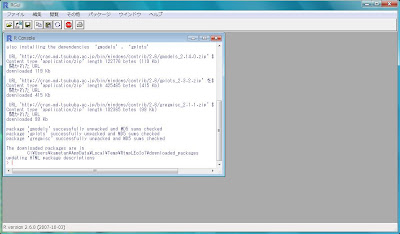
無事パッケージのダウンロードが終わります。

Linux版Rでのパッケージのインストール方法は、端末(ターミナル)で次のようなコマンドを入力します。

install.packages("ダウンロードしたいパッケージ")

例えば、今回Rcmdrが必要なワケですから、次のように端末のコマンドプロンプトに入力します。

install.packages("Rcmdr")

すると、R上で次のようにパッケージのダウンロードが始まります。

註:Ubuntu/Kubuntuの場合は、R経由でインストールするより、Synapticパッケージ・マネージャないしはAdeptパッケージ・マネージャ経由でインストールした方が確実かもしれません。

Rcmdrの起動方法

Rcmdr(Rコマンダー)はWindows版では、まずはRGui上部にある[パッケージ]プルダウンメニューから[パッケージの読み込み...]を選びます。

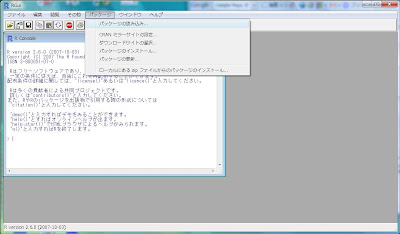
そうすると[1つを選択してください]ポップアップが出てきますので、パッケージの一覧から[Rcmdr]を探し出してクリックして[OK]ボタンを押します。

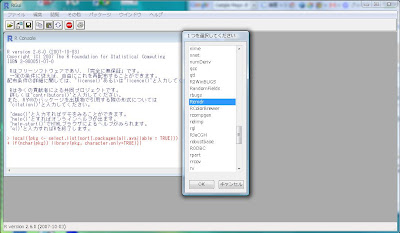
それにより、Rコマンダーが以下のように起動します。

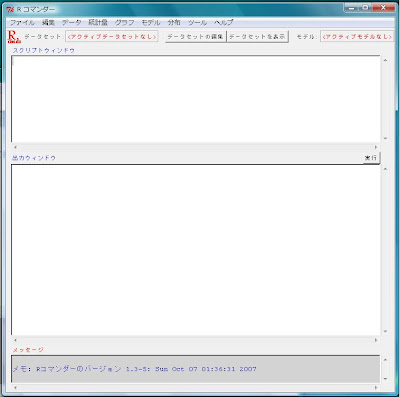
以降は、基本的に亀田はLinuxユーザーなので、Linux版の画面写真を元に解説していきますが、Rコマンダー及びRはLinux版でもWindows版でも全く同じように操作出来るので、ご心配は無用です。

Rcmdr(Rコマンダー)はLinux版では、コマンドラインで起動します。
端末(ターミナル)で次のように打って、Rcmdrを起動します。

library(Rcmdr)

そうするとRコマンダーが起動します。

これを使えば基本的なRの操作を全てマウスで行う事が出来ます。

Rcmdrでグラフ描画

Rcmdrの上部のプルダウンメニューに[分布]と言うモノがあります。
そこで大体のメジャーどころの確率分布の計算や描画が行えるようになっています。

	[分布]の内訳は正規分布を代表とする[連続分布]と二項分布を代表とする[離散分布]に分かれている。超幾何分布は後者なので、[離散分布]のツリーを辿っていく。 Rcmdrで扱える[離散分布]は二項分布ポアソン分布幾何分布超幾何分布負の二項分布の計5種類。これはRで扱える離散分布が5種類しかない、と言う意味ではなくって、単にGUI操作で扱う上で代表的な5種類をメニューに加えているに過ぎない。また、将来的にはこのメニュー内容がもっと充実する可能性もある。なお、今回は[超幾何分布を描く...]を取りあえず選ぶ。
	グラフデータ入力画面。それぞれの文字は超幾何分布を $p(x) = \frac{ \left( \begin{array} m \\ x \end{array} \right) \left( \begin{array} n \\ k-x \end{array} \right) }{ \left( \begin{array} m+n \\ k \end{array} \right) }$ としたモノに対応している。なお、[確率関数のプロット]で確率分布の描画を、[分布関数のプロット]で累積分布関数の描画を行う。
	グラフ出力の例。この例ではm＝4、n＝2、k＝3の超幾何分布の累積分布関数、としてみた。 3になった時点で「全ての可能なケースが足し合わされた」ので、1.0になる、と言う問題1.の意図が視覚的に確認出来る。

こんな感じで、R＋Rcmdrの組み合わせではいろいろな条件でのいろいろな確率分布/累積分布の作図がいとも簡単に出来てしまいます。

[GUI版R] R Commander の説明書

高校数学の窓LaTeX版

高校数学の窓過去問検索