高校数学の窓過去問検索

質問＜３６０９＞AAZ「確率変数の分布関数と確率密度関数」

以下質問文です

X、Yの同時確率密度関数が

    p(x,y)=k(x+y) (0≦x≦1,0≦y≦1)
      =0 (その他)

のとき、次の問いに答えよ。

  1. 定数kの値を求めよ。

  2. X,Yの周辺確率密度関数、をそれぞれ求めよ。

  3. X,Yの同時分布関数F(x,y)を求めよ。


★希望★完全解答★

ええと、ある意味凄く気持ち悪い問題だと思います(笑)。
まあ、実際はcqzypxさんが既に答えてくれているので、特に何ら書く事もないんですが、ある意味面白い問題だな、と思う部分もあるので、ちょっとしたアクロバットな方法論を紹介しておこう、と考えました。「数学じゃない」部分で解説するのもアリではないか、と(実際僕は数学らしい数学の話を書くことはめったにないのですが・笑)。

さて、ところで、実際問題、多重積分の問題としてはこの問題自体は大した問題ではありません。ただし、「2つの確率変数を扱った確率分布である」って前提が物凄く気持ち悪くなる原因なのです。
通常、多重定積分を行う場合、「積分する領域」を問題が示唆してくれたりするんですが、この問題の場合「それ」がありません。「確率分布である」と言う条件だけが提示されていて、それ以外は何もない。果して「確率分布である」と言う条件だけで積分領域がどう決まるのか、それがイメージしづらいのです。だから「気持ち悪い」。

確かに数学では「イメージする力」とか「想像力」が問われます。ところが、こういった問題の場合、その「イメージを掴む為の」とっかかりが見えない。そう言う理由で「多重積分の問題としては何て事が無い問題」が難問化するんですね。こりゃどーしようもねえ。

そこで。プログラムを書いて図示化する、って道を選びましょう。
普段の勉強に於いて、「どんな形であれ図示化しておく」練習をしておけば、いざと言うときこういう「掴み所が見えない」問題が出た時でも他の人よりは「想像力」を働かせる事が出来るでしょう。
また、実際、任意の二変数関数f(x,y)を用いた



の形の確率分布は「どーにでも捏造できる」モノです。ただし、このテのを専門的には正規化定数とか分配関数とか呼ぶんですが、一般にこのZは解析的に求まるかどうか分かりません。この問題の場合は当然「解析的に求まる」ワケですけど、あくまで「一般的に」その保証があるワケではないのです(ないしは凄く計算がシチメンド臭い、とか)。
こう言う場合、数理統計学者は一体どうしてるのか?と言う観点で、一種「最新技術」を紹介しておこうと思います。完全に「高校数学の」窓としては逸脱していますが(笑)、たまにはイイのではないか、と(笑)。また、理論面はどうあれ、高校生でも１回覚えておけば「バカの一つ覚え」で色々な確率分布を図示できるので、将来的な事を考えても有用な技術となるでしょう。今のうちに慣れておくに越した事ないです。

ところで、勘のイイ人だと、

「亀田と言えばコンピュータ・プログラム・・・・・・ああ、またモンテカルロ法でしょう?」

とか思うかもしれません。当たりです(笑)。ただし、今回は「ちょっと変わった」モンテカルロ法を行ってみます。
以前、モンテカルロ法を紹介した時に、

コンピュータを用いた乱数シミュレーションをモンテカルロ法と呼ぶ

と書きました。が、半分正解で半分違うんです。
実は「乱数を用いる」だけでなくって、「乱数をつくり出す」プログラムも広義では「モンテカルロ法」と呼びます。
つまり実際のトコ、「乱数絡み」のプログラムは全てモンテカルロ法、と呼んでも構わないのです。
この問題の場合、p(x,y)＝k(x+y)と言う「全くよくわからない確率分布」を相手にします。そして一般に、こういう「良く分からない」確率分布は無数に存在するんですね。
一方、そんな「良く分からない」確率分布でも、それが生成する「乱数」さえあれば、その確率分布がどういう形をしてるのか、平均は何なのか、分散はどんなモノなのか、それらの性質を知ることが出来ます。

「当たり前の事言ってるように聞こえるけど・・・・・・その確率分布そのものが"良く分からない"んじゃない?良く分からない確率分布から乱数を生成する?そんな事って出来るの?」

と思うでしょうが、実は出来るんです。
こういう「ちょっと特殊な、乱数を生成する為のモンテカルロ法」のうちの一つをメトロポリス法と呼びます。
今回はこのメトロポリス法を紹介したいと思います。専門書を買えば5,000円近くかかるネタなんですが(笑)、幸いこのサイトはタダなんで(笑)、ここでメトロポリス法を覚えたら絶対お得ですよ(笑)。さあ、お立ち会い(笑)!!!

方針

目的の1番目は、問題にある

p(x,y)=k(x+y)

と言う確率分布からそれに従う確率変数xとyの乱数列をメトロポリス法を用いて発生させる事です。
目的の2番目は、その乱数列xとyを用いて立体的な度数分布表(ヒストグラム)を作ります。これで「どういう形の確率分布なのか?」がハッキリと分かるでしょう。
なお、p(x,y)=k(x+y)に従う2つの乱数列を生成する為のプログラムはいつも通りDrSchemeを用いて記述しますが、それを図示化するには統計解析ソフトRを用います。と言うのも、DrSchemeはグラフィックス関係が弱い。その点、統計解析ソフトRは強力な作図機能を備えているので、データ(この場合はメトロポリス法で作った2つの乱数列)さえあれば、かなりラクにヒストグラムを作る事が出来ます。
一方、確かに全部の工程を統計解析ソフトRで行うことも可能ですが、正直、「プログラミング言語」としては統計解析ソフトRはあまりスマートではありません。少なくとも、個人的な意見では、DrSchemeの方が簡単で、かつ、キレイにプログラムを書く事が可能なので、頻雑さが無いのです。
よって、メンド臭く思うかもしれませんが、この2つのソフトの間で「ファイルをやり取り」した方が結果簡単だ、と言う事です。んで、思ったよりそれはメンド臭くないんで、心配しなくって大丈夫です。
なお、DrSchemeの基本的な使い方に付いては、ココやココに記述があるので、軽く目を通しておいてください。

メトロポリス法の基本


一応最初にメトロポリス法の概要を問題に従って説明したいと思います(こういう雛型提示を疑似コードと呼んだりします)。


  1. 0以上1以下の一様乱数を使ってp(x,y)＝k(x+y)に従う確率変数の初期値、を決める。

  2. 別の0以上1以下の一様乱数(random)を二つ使って、を計算式に従って作る。

  3. 、とする。(この問題設定上、、でなければならず、そうでない場合は7番に移る。)

  4. を計算する。

  5. また新しくの一様乱数Rを生成する。

  6. もし、なら生成した乱数を、として2番に戻って繰り返す。

  7. それ以外は、生成した乱数を、として2番に戻って繰り返す。


これがメトロポリス法です。実際は、2番〜７番のステップを延々と繰り返せばxの乱数列とyの乱数列が生成されて、それらはp(x,y)＝k(x+y)に従う乱数列となるのです。
注意点をいくつか。
まずはメトロポリス法内で扱う一様乱数は結構数が多いので、どれがどれなのか混乱しないようにしましょう。
また、

「あれ?p(x,y)＝k(x+y)自体はどうなったの?これは生成される乱数列にはならないの?」

と言う疑問を持つ人もいるかもしれません。これは、最初は勘違いするんですが(僕も一時期してました・笑)、その通りです。乱数列となるのはあくまで、xとyの方であって、p(x,y)＝k(x+y)は「枠組を提供する(wを計算する)為だけに存在して」て、「結果自体」にはならないのです。
と言うのも、通常の数学的な枠組では、x、yは独立変数であって、f(x,y)がそれによって計算される「確固とした関数」(従属変数)になることは確かなんですが、一方、確率分布と言うのは、そう言う意味では「数学的な関数」ではないんです。むしろ、「確率変数」と言う言い方をしますが、こっちの方が、ある種「関数」そのもの(計算結果)なんですね。何の関数かって?平たく言えば「運」の関数なんですよ(笑)。
つまり、確率分布p(x,y)＝k(x+y)と言う数式自体は「数学的な関数」を表しているワケでも何でもなくって、「運の関数」である確率変数x、yの「出方」を制御する「枠組」なんですね。実は確率分布の数式自体は「数学的な関数として」の意味は持ってないんです。x、yが決まったからp(x,y)が一意に決まる、なんて構造はそもそも持っていません。
たぶんこの解説読んでも最初はピンと来ないでしょうが(笑)、まあいずれにせよ、「大事な結果」はxとyの方です。この事だけは覚えておいてください。
なおはメトロポリス法のプログラム上は、外部引数として与えるモノとし、固定した値は持たせない事とします。


まずは核(kernel)を作る



さて、取り敢えずは一番簡単な部分から作り始めましょう。
DrSchemeを起動して、上部のエディタに次のように入力します。

    (define kernel
      (lambda (x y)
        (+ x y)))

これは数学的には次の関数を表しています。



これで問題の確率分布の表現は終わりです。
・・・・とか聞いて、

「え、でも、問題の確率分布はp(x,y)＝k(x+y)でしょ?kが消えちゃってるのはマズいんじゃないの?大体kを求めよ、ってのが題意でしょ?」

とか思う人もいるでしょうが、実はメトロポリス法に於いては、正規化定数の値は考慮しなくってイイのです。
「ええ?」って思うかもしれませんが、前出の疑似コードの4番を見てください。問題に従うと、



となって結局、正規化定数は約分されて消えてしまいます。
これはメトロポリス法の大きな特徴なんです。結果メトロポリス法に於いては全く正規化定数は関係無くなってしまうのです。
ちなみに、統計学的には用語が定まってないのですが、こう言った「確率分布の正規化定数以外の関数部分」をカーネル(核)と呼んだりする場合もあり、ここではそのカーネル、と言う単語を用います。
余談ですが、メトロポリス法を利用した実際の実装は殆んど無いのですが、例えば「解析的に積分が出来ない」確率分布にご存知正規分布があります。



この場合もカーネルは



と表現出来て、メトロポリス法を用いて正規分布に従う乱数(正規乱数)を作る事が出来ます。
メトロポリス法を覚えたら、是非とも実装してみてください。
なお、本題に戻ると、カーネルをDrSchemeに記述し終わったら、一旦ファイルを名付けて[保存]しましょう。



ここではファイル名をQ3609と名付けています。
そして、最終的に外部入力を促すQ3609と言う名前のプログラムを走らせて全ての計算をさせる、と言う意図があります。
次はそのQ3609と言うプログラムを書いてみましょう。

ダミーのプログラムQ3609を作る。



次にダミーのプログラムQ3609を作ります。
このプログラムは次の意図があります。

  1. 主な計算自体を行うプログラムは別にmetropolisと言う名前を付けて作る。

  2. 従ってQ3609は最小限の入力を人間(つまり僕等)から受け取ってそれをmetropolisに渡す役割、とする。

  3. また、metropolisが必要とする引数の初期値を渡す。


この3つの役割をQ3609に持たせる事、とします。
なお、ここでQ3609を走らせる際に人間側が入力する引数は、何回繰り返し計算をさせるか指定するnと、との変位の幅を決めるの二つ、とします。
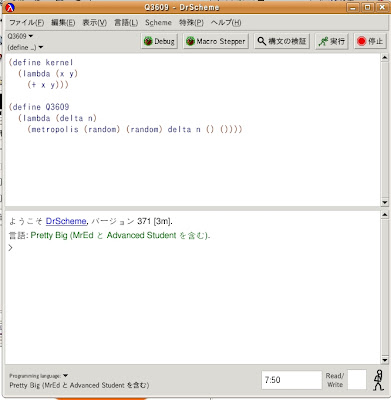
以上より、Q3609のコードは次のようになります。
    (define Q3609
      (lambda (delta n)
        (metropolis (random) (random) delta n ()())))

なお、(random)と言うのは、Scheme上で0〜1の範囲の範囲で生成される一様乱数で、これでx、yの二つの変数の初期値を与えます。
また()ってのを空リストと呼びます。つまり、この二つに生成されたxの乱数とyの乱数を突っ込んで行くのです。これも乱数列の初期値、と言う事ですね(初期値なんで何も中に入っていない、って事です)。
つまり、ここで分かるのは、プログラムmetropolisを走らせる際、その書式は

(metropolis x y delta n xのリスト yのリスト)

となっている、って事です(別にこのプログラム自体を表向きには走らせませんが)。
そして、例えばn＝10,000を与えると、動作としては

0回目:(metropolis delta 10000 () ())
1回目:(metropolis delta 9999 () ())
2回目:(metropolis delta 9998 ( ) ( ))
3回目:(metropolis delta 9997 ( ) ( ))
・・・・・・

となる事を示唆しているんです。目論見通り、計算の回数nが減るに従って、リスト内の乱数の要素が増えていく事が分かりますし、それによって2つの乱数列を得る事が出来るのが分かると思います。
取り敢えず、ダミープログラムQ3609を先ほど作ったプログラムを先ほど作ったエディタ(ファイル)Q3609のkernelプログラムの下に改行して書き込み[保存]しましょう。



なお、ここでScheme上でのリストの基本操作命令であるconsに付いてちょっと解説します。
consと言うのは、リストの先頭に要素を追加する命令です。以下がその書式です。

(cons 要素 リスト)

これにより、リストの先頭に要素を追加する事が出来ます。
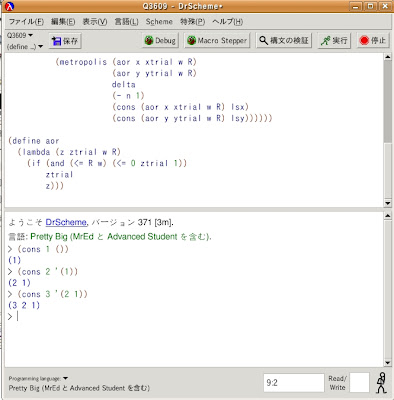
例えば、これはDrSchemeの下段のインタプリタで実際実験して欲しいんですが、次のような命令をプロンプトの後に書いてみて、どうなるか[実行]してみてください。

(cons 1 ())
(cons 2 '(1))
(cons 3 '(2 1))



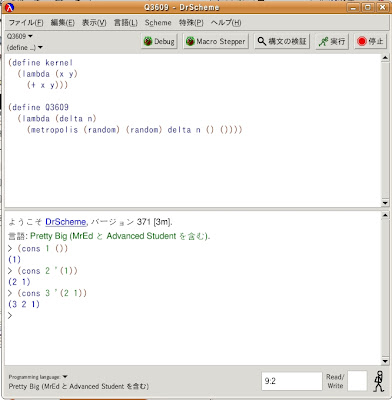
はい、ご覧の通り、先頭に新しい要素を付け足したリストが作られますね。

註:なお、'はScheme用語でクオートと呼び、「これは単なる数字じゃないですよ」と言うサインを表しています。要するに、これで「リストです」と表現しているワケです。

このconsと言う命令が計算の本体であるプログラム、metropolisのある意味鍵を握ります。

メトロポリス法の実行エンジン、metropolisを作る



さて、いよいよ計算の本体、プログラムmetropolisを書いてみましょう。
プログラムmetoropolisも再帰と言う枠組で作ります。
ここでもう一度再帰の枠組を説明しておきましょう。

  1. n＝0の時、metropolis法の実行結果を返す。

  2. nが任意の自然数kの時、n＝k−1の時のmetropolis法の実行結果に対し、n＝kの時のmetropolis法の実行結果を適用する。


これだけ、です。
もう一度言いますが、これは数学的帰納法(ないしは数列/漸化式)の枠組とまるっきり同じだ、と言うことです。

  1. P(0)は真である。

  2. 任意の自然数kに対し、P(k)が真であれば、P(k+1)も真である。


全く同じ構造ですね。
つまり、こういう再帰、と言うプログラム法を学ぶ事により、数学的帰納法/数列/漸化式が苦手な人が結構多い(僕もそうですが・笑)んですが、「ああ、こういう考え方って使えるよな」と感じてほしい。そのテの数学的な考え方に慣れる為にはSchemeと言うプログラミング言語は絶好の武器なんですよ。高校生〜大学生の為の数学の自習向きのプログラミング言語、と言えます。
さて、再帰の枠組の1番に従って、「一体計算結果として何を返すのか?」考えます。取り敢えず暫定的にxの乱数列のリストとyの乱数列のリストの2つを要素としたリストを返すように設定してみましょうか。つまり「リストのリスト」を返すように設計してみましょう。
すなわち、

n＝0の時、(list xの乱数列のリスト yの乱数列のリスト)を返す

と取り敢えず置いてみます。なお、listと言う命令はリストを作る命令です。
あとは再帰の枠組の2番を考慮して、k番目のメトロポリス法をk−1番目のメトロポリス法の計算結果を用いて定義してやれば一丁上がりです。
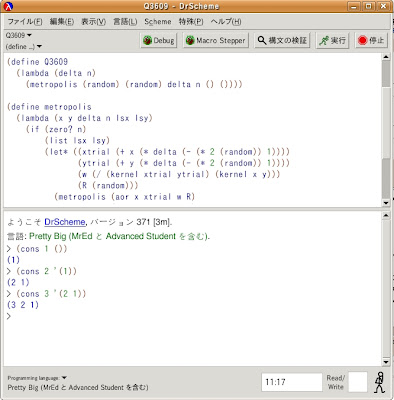
以上を考慮して、プログラムmetropolisは次のようになります。

    (define metropolis
      (lambda (x y delta n lsx lsy)
        (if (zero? n)
          (list lsx lsy)
          (let* ((xtrial (+ x (* delta (- (* 2 (random)) 1))))
            (ytrial (+ y (* delta (- (* 2 (random)) 1))))
            (w (/ (kernel xtrial ytrial) (kernel x y)))
            (R (random)))
          (metropolis (aor x xtrial w R)
            (aor y ytrial w R)
            delta
            (- n 1)
            (cons (aor x xtrial w R) lsx)
            (cons (aor y ytrial w R) lsy))))))


意外に簡単なコードになったな、と思わないでしょうか?(まあ、そう感じなくても構いませんが・笑。しかし、他の言語だったらもっと複雑な形になったりします。)
取り敢えず、ここまでエディタ(Q3609ファイル)に書き込んで、そして[保存]しましょう。



なお、ある意味モンテカルロ法ってのはワンパターンなんで、一つ様式を覚えてしまえば他の問題にも簡単に転用出来ます。
が、ここで2つだけプログラムmetropolisに関してポイントを解説します。
一つ目は局所変数let*です。これは基本的には＜質問3590＞に出てきた局所変数letと同じモノです。これで定義された変数はプログラムmetropolisが1回実行されて終了するまでの範囲だけで有効なんです。つまり、1回metropolisが起動終了してしまえば、そこで定義された変数は廃棄されてしまいます。
「それが何か?」と思うかもしれませんが、こういう事です。つまり、k−1回目のメトロポリス法で使われた局所変数とk回目のメトロポリス法で使われる局所変数は同じ数ではない、と言う事です。これが意味するのは、「局所変数」と言うのは繰り返し計算の過程に於いて「どんどん書き換わっている」んですね。これが大事な性質なんです。
ここで定義されている局所変数は、数学的には次の4つです。






この四つはメトロポリス法の基本を鑑みれば分かると思いますが、「1回の計算が終わる度」書き換わらなければならない変数です。従ってlet*を使って局所変数として定義してるんですね。プログラム上の表記法と数学的な表記法は違いますが(例えばはmetropolis内ではxtrialと表記されています)、let*内の局所変数の定義と良く見比べて下さい。「全く同じ事を表現している」と言うのが分かるはずです。
なお、letとlet*の違い、と言うのは、たった一つで、letの場合は、局所変数内で定義された数を使って他の局所変数を定義出来ないのですが、let*の場合はそれが出来る、と言う部分です。
上の4つの式を見てもらいたいんですが、単純にwを定義するにあたって、別の局所変数とを参照しています。これはletに於いては許されていないんで、代わりにlet*を使っている、と。それだけなんです。
二つ目のポイントはプログラムaorです。k−1回目のメトロポリス法に「何かした結果」は、このプログラムaorを呼び出す事によって、

(metropolis (aor x xtrial w R) (aor y ytrial w R) delta (- n 1) (cons (aor x xtrial w R) lsx) (cons (aor y ytrial w R) lsy)

と記述することが出来るワケですが(consの使い方にも着目!)、実はこのプログラムaorはまだ定義していません(笑)。
よって、今からこのプログラムaorを記述します。

プログラムaorを作る



AORと聞くと、音楽が好きな古い世代の人たちは

「Adult Oriented Rock???」

とか思うでしょうが(古い話ですんません・笑)、全然関係ありません(笑)。いや、昔は(８０年代初頭くらい?)湘南辺りのサーファーとかAORってジャンルの音楽を良く聴いてたらしいです(笑)。
ええと、別にプログラムの名前をどう付けようが構わないんですが(笑)、ここでのaorの意味はaccept or rejectの省略形です。accept(受諾)かreject(棄却)か、って意味ですね。
メトロポリス法の基本の６番、７番にあたる仕事ですが、結局xであろうとyであろうと、acceptとrejectの仕事そのものはどっちの変数だろうと変わりません。よって、ここで汎用のプログラムaorを書いてしまおう、と言うのが狙いです。
ここではx、y、xtrial、ytrialに使える汎用の変数をz、ztrialと名付けて、次の事柄をプログラムaorに翻訳します。

  1. かつ、の時はを使用。

  2. それ以外はを使用。

これをif構文を利用して次のように書きます。

    (define aor
      (lambda (z ztrial w R)
        (if (and (<= R w) (<= 0 ztrial 1))
          ztrial
          z)))


これも単なる基本的なif構文ですが、ポイントを二つほど。
まずは関数andですが、これは

(and 命題1 命題2 命題3 ....)

と複数の命題を並べ、全ての命題が真だった時、「真」を返します。そんなに難しくありませんね。
ここでは(<= R w)と言う命題と(<= 0 ztrial 1)と言う命題の2つが同時に真になるかどうか判定する役割を担っています。 二つ目のポイントは<=と言う命令です。これは「以下」かどうか調べる役割を担っています。 通常のプログラミング言語ですと、0以上１以下なんかを一行で記述するのは難しいのですが、生憎Schemeは前置記法を採用している為、(<= 0 ztrial 1)なんて書き方でを確かめる事も出来ますし、また、もっと複数の数の大小関係を調べるのもたった１行で書けるんです。
さて、エディタ(Q3609のファイル)にプログラムaorを書き込んで[保存]しましょう。



これで取り敢えず今回の問題に準拠したメトロポリス法の雛型は完成致しました。

メトロポリス法のソースコードを見てみる



今までの工程は初心者に対しては複雑に見えるでしょうから、一旦、プログラムQ3609の全体(ソースコード)をもう一回見てみましょう。

    (define kernel
      (lambda (x y)
        (+ x y)))


    (define Q3609
      (lambda (delta n)
        (metropolis (random) (random) delta n ()())))


    (define metropolis
      (lambda (x y delta n lsx lsy)
        (if (zero? n)
          (list lsx lsy)
          (let* ((xtrial (+ x (* delta (- (* 2 (random)) 1))))
            (ytrial (+ y (* delta (- (* 2 (random)) 1))))
            (w (/ (kernel xtrial ytrial) (kernel x y)))
            (R (random)))
          (metropolis (aor x xtrial w R)
            (aor y ytrial w R)
            delta
            (- n 1)
            (cons (aor x xtrial w R) lsx)
            (cons (aor y ytrial w R) lsy))))))


    (define aor
      (lambda (z ztrial w R)
        (if (and (<= R w) (<= 0 ztrial 1))
          ztrial
          z)))

基本的にはプログラムQ3609は4つのパーツによって構成されています。
そしてこれらは、

    Q3609→呼び出し→metropolis→呼び出し→kernel
            ↓
            呼び出し
            ↓
            aor


と言う依存関係になっています。
これら4つのパーツを同一ファイルに書き込む事によって、特にこちら側で何か設定しなくても、お互いが必要な時に必要なモノとして呼び出されて一つのプログラムのように動いてくれるのです。
では、実際にプログラムQ3609を走らせてみましょう。
[実行]ボタンを押してください。

Q3609を走らせてみる



Q3609の実行方法は、DrSchemeの下段のインタプリタのプロンプト以降に、Schemeの流儀に従って前置記法で次のように入力して[Enter]キーを叩きます。

(Q3609 delta 試行回数)

ここで、の値をどうするか、ですが、基本的には何でも構わないんですが、今回の問題のx,yの変位の幅「1」の大体三分の一から二分の一辺りが適当だと思います。すなわち0.3〜0.5くらいを与えれば良い。ここではくらいにしてみましょう。
また試行回数ですが、これも自由にして頂いて結構です。大体10,000回も走らせればイイのではないでしょうか?
取り敢えず亀田は100万回くらい走らせてみます。つまり、命令は

(Q3609 0.4 1000000)

としてみます。
以下の写真が実行結果ですね。



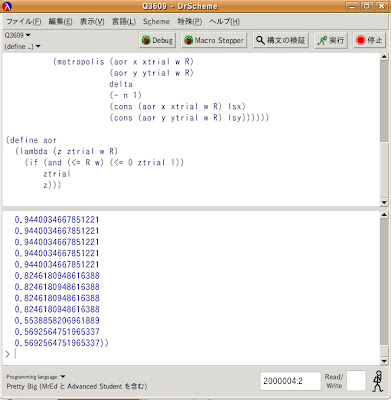
100万回もループさせるとさすがに実行時間がかかり、途中「止めときゃ良かった」とか思いましたが(笑)、一応計算は終了しました。
基本的に

((100万個のxの乱数列) (100万個のyの乱数列))

と言う形で出力されています。
が。色々乱数列を眺めて楽しむのもイイんですが、100万個×2列の乱数をただ眺めていたって何がどうなる、ってワケではありません。仮に1万個×2だとしても、人間が分析するには当たり前ですが、量が多すぎるのです。
そこで。こういう「メトロポリス法」で行った計算結果をファイルとして出力し、他の画像描画ソフトに渡してそこで作図させる作戦を取ります。つまり、今まで書いたQ3609のプログラムを若干手直しして改造します。
その前に「どう言ったファイルを作成させればいいのか?」ちょっと説明したいと思います。

CSVファイルと言う形式


ちなみに、基本的にパソコン上ではどんなデータでも原則文字だらけなんです。音声データだろうが、画像データだろうか、動画データだろうが、実は元々文字だらけのファイルなんですね。
「うそ!?」って思うかもしれませんが、原理的にはそうなんです。ただし、その「文字列」を記入したテキストファイルを「固有のフォーマット」に従って作成して、「適切な拡張子」を付加して定義する。例えば最近有名な音声データであるmp3ファイルなんかも原理的にはそうやって作られています。
さて、そんな中で純粋なテキストファイルとしてはこれまた色々なデータの記述方式があるんですが、その中でメジャーなモノにCSVファイルと呼ばれる形式があります。この形式のファイルは例えばMicrosoft Excelなんかでも表計算用データとして開く事も可能ですし、と言うことはMicrosoft Excelに読み込ませて作図させる事も可能です。
もっとも今回は統計解析ソフトRを用いる、と言う前提なんで、Microsoft Excelは用いません。大体、ちょっと多めのデータ(例えば1万件以上のデータ)を扱うとなるとMicrosoft Excelだと簡単にバグりますし、また描画も困難になるから、です。まあ、興味があったら、あとで自分で実験してみてください。
ところでCSVファイル形式、とは言っても実はそんなに作成が難しいファイル形式ではありません。以上の3点を満たせばCSVファイル、ってのは簡単に作成出来るんです。

  1. ファイルの拡張子は.csvとする。

  2. 列単位のデータの区切りはコンマ(,)を用いる

  3. 行単位のデータの区切りは改行で表す

これだけ、です。意外に大した事ないでしょ(笑)?まあ、それだからこそ色々なソフトの間で「データの互換性を取るために」使われているワケですが。
具体例を見てみます。CSV形式では次のようなデータの並べ方をします。

,
,
,
,
......
,
このようにコンマで区切って対応するデータ同士を並べていけば良い。
これで乱数列をどうやってCSV形式に変換するか大体のトコ分かりました。
では実際に出力用のSchemeプログラムを書いてみましょう。

出力用プログラムwrite-lsを作る



取り敢えず、出力用プログラムのwrite-lsがどうなるか、書いてみましょう。

    (define write-ls
      (lambda (lsx lsy)
        (if (or (null? lsx) (null? lsy));1、2参照
          (newline);3参照
          (and (display (car lsx));4、5参照
            (display ",")
            (display (car lsy))
            (newline)
            (write-ls (cdr lsx) (cdr lsy))))));6参照


実はこのプログラムwrite-ls自体も再帰構造で書かれています。
基本的なアイディアは以下の通りです。

  1. xの乱数列、またはyの乱数列が無くなった時、改行して終了する。

  2. それ以外では、xの乱数列の先頭を印字、コンマ(,)を印字、yの乱数列の先頭を印字、改行してwrite-lsをそれぞれの乱数列リストの残りに対して適用する

これだけ、です。
ではポイントをいくつか解説します。

  1. OR関数:
    書式は

    (or 命題1 命題2 命題3 ...)

    と複数命題を並べる事が出来ます。命題のうちのどれかが真だった場合、真を返します。
    ここでは(null? lsx)と(null? lsy)と言う命題のうちのどちらかが真かどうか調べています。

  2. null?関数:
    リストが空リストかどうか調べる関数です。空リストであった場合真を返します。
    書式は

    (null? 判定したいリスト)

    となります。

    例:(null? ())→真
    (null? '(1 2 3))→偽


  3. newline関数:
    改行するための命令です。書式は

    (newline)

    です。

  4. display関数:
    出力/表示の為の関数です。書式は

    (display 表示させたいモノ)

    です。「表示させたいモノ」は計算結果だろうと文字だろうと構いませんが、文字を表示する場合はダブルクオテーションマーク(")で挟みます。

    例:

    • (display (+ 2 3))→「5」を表示

    • (display "Hello!")→「Hello!」と表示


    • car関数:
      リスト基本操作関数のうちの一つ。car関数はリストの先頭要素を返します。
      書式は

      (car 先頭要素を返したいリスト)

      です。

      例:(car '(1 2 3))→「1」を返します。

    • cdr関数:
      リスト基本操作関数のうちの一つ。cdr関数はリストの先頭要素「以外の」リストを返します。
      書式は

      (cdr 先頭要素以外を返したいリスト)

      です。

      例:(cdr '(1 2 3))→(2 3)を返します。

    これが出力用のプログラム、write-lsの全てです。
    ではこれを用いてプログラムQ3609の改造を行います。
    取り敢えずエディタ(Q3609のファイル)にプログラムwrite-lsを書き込んで[保存]しましょう。



    プログラムQ3609をCSVテキストファイルを出力出来るように改造



    まずは、もう一回全ソースコードを見て改造されたポイントを書いていきます。
    なおセミコロン(;)以降はコメントと言ってプログラム本体の実行には何の影響もありません。

      (define kernel
        (lambda (x y)
          (+ x y)))


      (define Q3609
        (lambda (fname delta n);引数fnameを追加
          (with-output-to-file fname;新しい関数追加
            (lambda ();ここの引数は無し
              (metropolis (random) (random) delta n ()())))))


      (define metropolis
        (lambda (x y delta n lsx lsy)
          (if (zero? n)
            (write-ls lsx lsy);list関数の代わりに出力用関数write-lsを採用
            (let* ((xtrial (+ x (* delta (- (* 2 (random)) 1))))
              (ytrial (+ y (* delta (- (* 2 (random)) 1))))
              (w (/ (kernel xtrial ytrial) (kernel x y)))
              (R (random)))
            (metropolis (aor x xtrial w R)
              (aor y ytrial w R)
              delta
              (- n 1)
              (cons (aor x xtrial w R) lsx)
              (cons (aor y ytrial w R) lsy))))))


      (define aor
        (lambda (z ztrial w R)
          (if (and (<= R w) (<= 0 ztrial 1))
            ztrial
            z)))


      (define write-ls
        (lambda (lsx lsy)
          (if (or (null? lsx) (null? lsy))
            (newline)
            (and (display (car lsx))
              (display ",")
              (display (car lsy))
              (newline)
              (write-ls (cdr lsx) (cdr lsy))))))


    基本的に改造するプログラムはQ3609とmetropolisの二箇所だけ、です。
    まず、最初のポイントとしては、Q3690が外部から受け取る引数はfname、、試行回数nの3つとなり1つ増えています。なお、fnameってのはfilenameの省略形です。Q3609は出力するCSVファイルの名前を入力するように改造されたのです。
    次のポイントは、最初書いたmetropolisでは最終的には(list lsx lsy)と言う命令によって「2つの乱数列リストのリスト」を返すように設計していました。これを先ほど作った新しいファイル出力用関数write-lsを用いて改造しています。今度はリストとして出力するのではなく、「CSVファイルとして」出力するのが目的だから、です。
    最後のポイントがwith-output-to-file関数です。これがプログラムwrite-lsの出力をファイルに書き込む役割を担っています。書式は

    (with-output-to-file ファイル名 (lambda () 作業内容))

    となり、これをダミープログラムQ3609に組み込ませたわけです。

    現時点では次のような作成したプログラム同士の呼び出しが行われています。

              write-ls
              ↑
              呼び出し
              ↑
      Q3609→呼び出し→metropolis→呼び出し→kernel
              ↓
              呼び出し
              ↓
              aor


    これでQ3609でCSVファイルを生成/出力が出来るようになりました。
    では、一旦ファイルを[保存]して[実行]ボタンを押してみましょう。



    Q3609を走らせてCSVファイルを生成する



    では、Q3609を走らせて乱数データを記述したCSVファイルを実際作成してみましょう。
    引数が一つ増えているので、Q3609の実行コマンドは以下のようになります。

    (Q3609 出力ファイル名 delta n)

    なお、注意事項としては、「出力ファイル名」は文字列データなので、ファイル名はダブルクオテーション(")で挟まなければならない、と言う約束事があります。
    また、必ず拡張子(.csv)を名前の後に付けるのを忘れないようにしましょう。
    ここでは出力ファイル名を"data.csv"と名付けて、、試行回数n＝100万回として次のようにDrScheme下段のインタプリタのプロンプトに入力して[Enter]キーを打ちます。

    (Q3609 "data.csv" 0.4 1000000)

    では結果を見てみましょう。



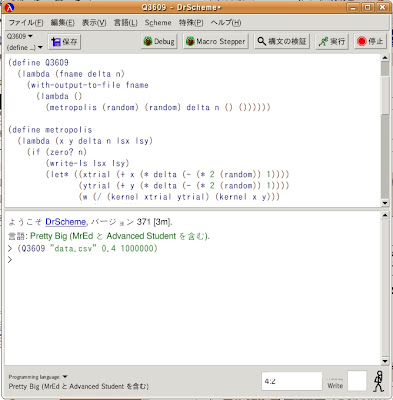
    ・・・・・・何も表示されませんね(笑)。
    「失敗したか?」と思うかもしれませんが、いや、計算/ファイル出力は成功してるんで心配しないでください(笑)。キチンとプロンプト(>)が一つ増えています(これは計算が終わった事の証)。
    また、「インタプリタ上に」計算結果を羅列するより早く動作を終えています。実はDrSchemeの場合、計算結果をインタプリタで表示する方が時間がかかるのです。そしてこれが意味するのは、実は先ほど実験した「100万回での試行実験」でも、計算そのものは比較的すぐ終わるんですが、「インタプリタ上への計算結果の羅列」の方にバカみたいに時間が取られている、って事です。意外なんですがテキストファイルへの出力の方が早く作業が終わるんですね。
    では、生成したファイルをチェックしてみましょう。Windows版のDrSchemeの場合、デフォルトではファイルの生成先はユーザーフォルダ内の自分のフォルダ内のドキュメントフォルダ内に生成されていると思います。



    パスで書くと

    C:\Users\******\Documents\data.csv

    となってる筈です(******はユーザー名)。
    Linux版の場合は、homeディレクトリ内の自分のディレクトリにCSVファイルが生成されていると思います。



    ではそのCSVファイル(data.csv)をマウスで右クリックして、テキストエディタ(Windows版ではメモ帳かWordpad)で開いてみましょう。

    註:恐らくダブルクリックで開こうとすると、WindowsではMicrosoft Excelを使って開こうとする筈です。それでも構いませんが、今回亀田が試したような100万回での試行ですと、完全にMicrosoft Excelが扱えるデータ量の範疇を越えてしまうので、どのみち単なるテキストエディタで開いた方が無難です。






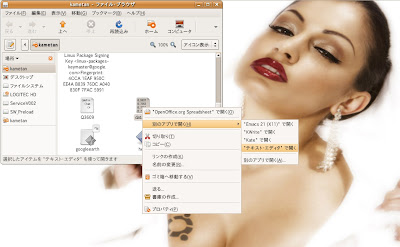
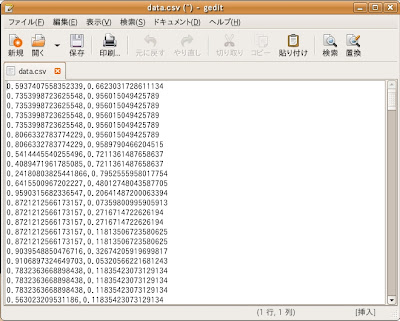
    ご覧のように"data.csv"をテキストエディタで開くと、xの乱数列とyの乱数列がコンマ(,)で区切られた状態で2列に渡って記入されている事が分かります。成功です。
    以上でDrSchemeでの作業は終わりです。
    ここから統計解析ソフトRに作業が移ります。

    統計解析ソフトRのダウンロードとインストール



    Rもタダで手に入るオープンソースの統計解析用ソフトウェアです。強力な統計関数とグラフィック関係のデバイスが含まれているので、この機会にダウンロード/インストールしてみましょう。

    ダウンロード&インストールの方法:

    ※:Rの最新版は2.6.0です(2007年10月5日現在)。


    それぞれのOS用の指示に従ってダウンロード/インストール/初期設定を行ってください。

    Rの起動



    Windows版の場合はダウンロード/インストールが終わるとデスクトップ上にRのアイコンが出来てる筈なので、それをダブルクリックすればRが立ち上がります。





    Linux版の場合は、まずは端末(ターミナル)を起動します。





    コマンドプロンプトにただRと大文字で打ち込むだけでRが端末上で起動します。



    パッケージのインストール



    Rの優秀なトコロは、数々の特殊な機能をまとめたプログラム群を追加インストール可能である、と言う部分です。これをパッケージと呼びます。
    今回利用するパッケージはRcmdrと言うパッケージとgregmiscと呼ばれるパッケージの2種類です。
    特にRcmdrと言うパッケージはコマンドラインバリバリのRにマウス操作の為のGUI環境を加える為のモノでこれは結構重宝します。詳しくはこのPDFに書いてあるので、参考にして下さい。マウスだけで基本的なRの操作が出来るようになります。

    Windows版Rでのパッケージのインストール方法は、RGui上部にある[パッケージ]プルダウンメニューから[パッケージのインストール...]を選びます。



    そうしたら、「どこのミラーサイトからダウンロードするのか?」尋ねてくる[CRAN mirror]ポップアップが出て来ます。



    現時点では日本のRのダウンロード先は



    の3箇所となっています。近場の大学のサイトをクリックして[OK]ボタンを押しましょう。



    そうすると、インストール可能なパッケージのリスト、[Packages]ポップアップが出てきます。スクロールして、目的のパッケージを探し出してクリック、そして[OK]ボタンを押してください。



    無事パッケージのダウンロードが終わります。

    Linux版Rでのパッケージのインストール方法は、端末(ターミナル)で次のようなコマンドを入力します。


    install.packages("ダウンロードしたいパッケージ")


    例えば、今回Rcmdrとgregmiscが必要なワケですから、次のように端末のコマンドプロンプトに入力します。


    install.packages("Rcmdr")
    install.packages("gregmisc")


    すると、R上で次のようにパッケージのダウンロードが始まります。




    註:Ubuntu/Kubuntuの場合は、R経由でインストールするより、Synapticパッケージ・マネージャないしはAdeptパッケージ・マネージャ経由でインストールした方が確実かもしれません。


    Rcmdrの起動方法


    Rcmdr(Rコマンダー)はWindows版では、まずはRGui上部にある[パッケージ]プルダウンメニューから[パッケージの読み込み...]を選びます。



    そうすると[1つを選択してください]ポップアップが出てきますので、パッケージの一覧から[Rcmdr]を探し出してクリックして[OK]ボタンを押します。



    それにより、Rコマンダーが以下のように起動します。



    以降は、基本的に亀田はLinuxユーザーなので、Linux版の画面写真を元に解説していきますが、Rコマンダー及びRはLinux版でもWindows版でも全く同じように操作出来るので、ご心配は無用です。

    Rcmdr(Rコマンダー)はLinux版では、コマンドラインで起動します。
    端末(ターミナル)で次のように打って、Rcmdrを起動します。


    library(Rcmdr)





    そうするとRコマンダーが起動します。



    これを使えば基本的なRの操作を全てマウスで行う事が出来ます。
    ではいよいよDrSchemeのメトロポリス法で作成したCSVファイルをRコマンダーを使ってRに読み込んでみましょう。

    Rコマンダーでデータのインポート



    RコマンダーでデータをインポートするにはRコマンダー上部の[データ]プルダウンメニューから[データのインポート]→[テキストファイルまたはクリップボードから]を選びます。



    そうすると[テキストファイルまたはクリップボードからデータを読み込む]ポップアップが表れます。



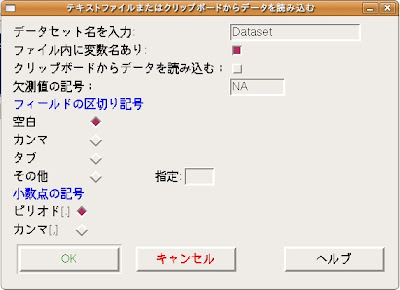
    ここでは次のように設定をします。









    1. データセット名を入力:好きな名前を入力して構いません。ここではデフォルトのまま"Dataset"とします。

    2. ファイル内に変数名あり:ファイル内に変数名は付けていないので、このチェックボックスは外します。

    3. フィールドの区切り記号:CSVファイルはフィールドをコンマ(,)で区切っているのでカンマを選びます。

    4. 以上の設定が終わったら[OK]ボタンを押します。





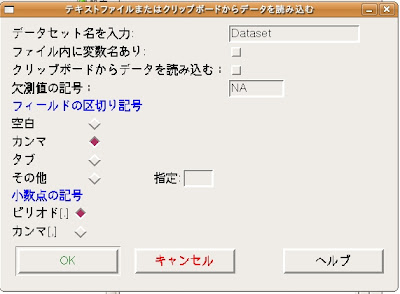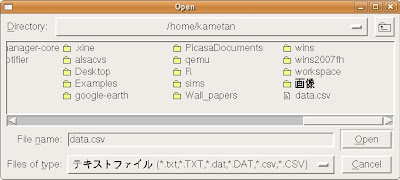    [Open]ポップアップが開くので、先ほどDrSchemeで作ったCSVファイル(data.csv)を捜し出して指定し、[Open]ボタンを押します。



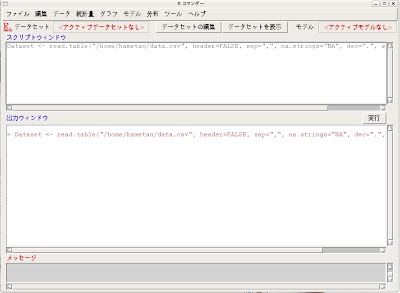    そうすると、data.csvがRに読み込まれます。


    では、ホントにdata.csvがRに無事読み込まれたかどうか確認してみましょう。
    Rコマンダーの上部に[データセットを表示]と言うボタンがあります。それをクリックしてみます。



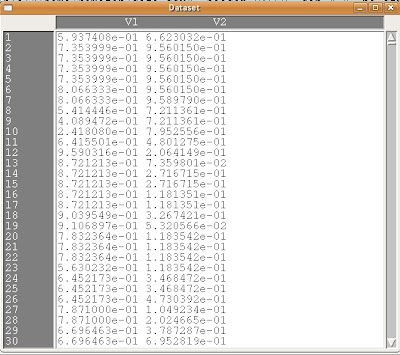
    そうすると上の図のようなポップアップが表れます。キチンと読み込まれていますね。こうなったらもう鬼の首を取ったも同然です(笑)。
    ちなみにxの乱数列はV1と言う列に格納されていて、yの乱数列はV2と言う列に格納されているのを確認しておいて下さい。
    ではポップアップを閉じてください。次の作業へと移ります。

    R上でのデータの扱い方



    Rでのデータは基本的にはベクトルとして扱います。
    今ここに、DatasetのV1列にxの乱数列が存在し、そしてV2列にyの乱数列が存在することが分かっています。取り敢えずこれらをxを言うデータベクトルとyと言うデータベクトルにそれぞれ格納しなければなりません。
    ここで初めてRコマンダー上でコマンドラインを用います。Rコマンダーの上段のスクリプトウィンドウに次のように記述して下さい。


    x <- c(Dataset\$V1)
    y <- c(Dataset\$V2)


    これはxとyにDatasetのV1とV2をベクトルとして代入せよ、と言った様な意味です。
    今回は細かく説明しませんが、基本的にRでは、代入をするときは＝記号の代わりに<-を用います。また、ベクトルをc()と言う書き方をします。そして何々と言うデータセットの何々と言うデータ、と表現する場合、上のようにドル記号(\$)で「〜の」を表現します。

    そして、上図のようにコマンドをスクリプトウィンドウに書いた後、それらのコマンドをマウスで選択し、右クリックボタンを押した後、[実行]を選びます。



    そうすると、下段の[出力ウィンドウ]に「命令を実行したよ」と言う意味で入力→実行したコマンドが表記されます。
    気になるんでしたら、xないしはyの文字だけ選択して同じように右クリックで[実行]してみてください。xデータベクトルの中身やyデータベクトルの中身が下の[出力ウィンドウ]にズラズラ出力される筈です。

    Rコマンダーでgregmiscパッケージを読み込ませる



    まずは3D描画をする前に下準備です。
    先ほどダウンロードしておいたgregmiscパッケージをRコマンダー上で有効にします。
    Rコマンダー上部に[ツール]プルダウンメニューがあるので、それから[パッケージのロード]を選んで下さい。



    そうすると、下の図のように[パッケージのロード]ポップアップが表れるので、そのパッケージリストの中からgregmiscを捜し出して、選択、[OK]ボタンを押してください。



    これでヒストグラムの3D描画の為の準備は完了です。

    3Dのヒストグラムを描く



    ここからは舟尾暢男さんのR-Tips辺りからコードをパクって来ます(笑)。
    次のコードをコピーして、Rコマンダーの上部の[スクリプトウィンドウ]にペーストし、そしてそのコードをマウスで選択→右クリックで実行して下さい。




        h2d <- hist2d(x, y, show=FALSE, same.scale=TRUE, nbins=c(20,30))
        persp( h2d\$x, h2d\$y, h2d\$counts,
               ticktype="detailed", theta=60, phi=30,
               expand=0.5, shade=0.5, col="cyan", ltheta=-30)






    そうしたら3Dのヒストグラムが生成される筈です。



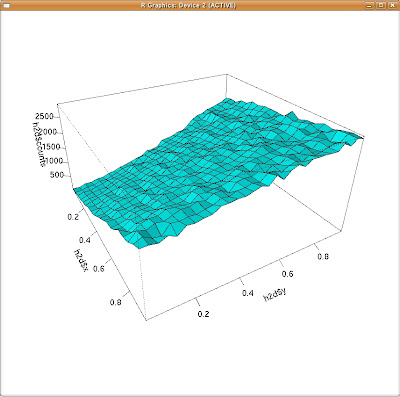
    はい、こういう感じの度数分布になってるんですね。これがメトロポリス法で作成した乱数列2つを用いたヒストグラムです。(まだデコボコしてますが、極限では平面になりそうだ、って事まで分かります!)
    最初に「多重積分の問題としては非常に簡単だ」と書きました。ただし、積分領域がイメージしづらいだろう、と。
    んで、多分AAZさんも実際に色々な積分領域を試したんでしょうが、「どれもピンと来なかった」ってのがホントのトコだと思います。
    実はメトロポリス法に依る実験ですと、要するに、と言う「凄くオーソドックスな」積分領域で構わないのです。そしてその多重積分が確率分布の性質、を満たすとすると、kは1にならざるを得ないのです。お分かりでしょうか?
    多分直感的にはx+yの分布は「一様分布みたいになるんじゃないか?」と思ってたんでしょう。自分の直観と相反する計算結果だったのが戸惑いの原因、「気持ち悪さの原因」だったのではないか?
    しかしながら、メトロポリス法でk(x+y)の分布を見る限り、「一様分布」と言う直感は否定されて、実はx=1、y=1に近づけば近づく程、「その目の出現の確率」が高くなっていくんです。逆にx=0、y=0に近づく程、「その目の出現の確率」は低くなっていくのです。面白いですね(笑)。
    これがcqzypxさんが書かれた回答のコンピュータ実験的な図示化なのです。

    周辺分布を見てみる



    では次に周辺分布を見てみましょう。とは言っても考え方は3Dのヒストグラムより簡単です。
    単純に言うと、の周辺分布とは、データベクトルxだけのヒストグラムの事を指します。
    また、も同じく、データベクトルyだけのヒストグラムですね。
    Rコマンダーで単純なヒストグラムを作るには、上部の[グラフ]プルダウンメニューから[ヒストグラム]を選べばイイだけです。



    そうすると[ヒストグラム]ポップアップが表れます。



    [変数]に表示されているV1(xの乱数列)、V2(yの乱数列)から任意の変数を選んで下さい。
    また、[軸の尺度]もどれを選んでも構いません。ここではデフォルトの頻度の計算を選んでみましょう。






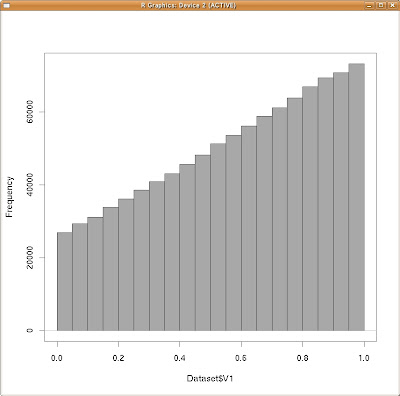    xの周辺分布(ヒストグラム)



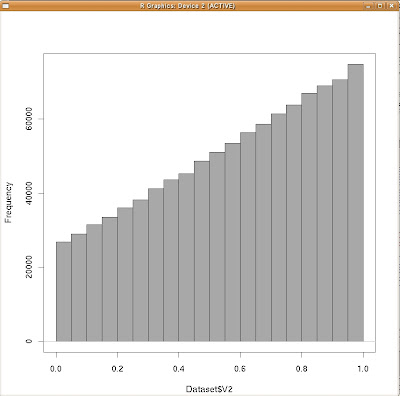    yの周辺分布(ヒストグラム)

    まあ、大して変わり映えのしないグラフが二つ出来ただけ、ですが(笑)。
    ところで、周辺分布の「頻度の高さ」と言うのは、一般に3Dのヒストグラムより高くなります。
    と言うのも当然で、「周辺分布を作る為の積分操作」と言うのは、例えばxの周辺分布を作るには、あるxの値に従ってy軸方向に散らばった「全てのデータ」を足しあげる、って事です。
    また、yの周辺分布に付いてもそうですよね。x軸方向に散らばったあるyに従ったデータを「全て足しあわせて」いるのです。
    こういう「積分操作の意味」と言うのも図解の方が分かり易いと思います。
    念の為に密度表示でもグラフを作ってみましょうか。







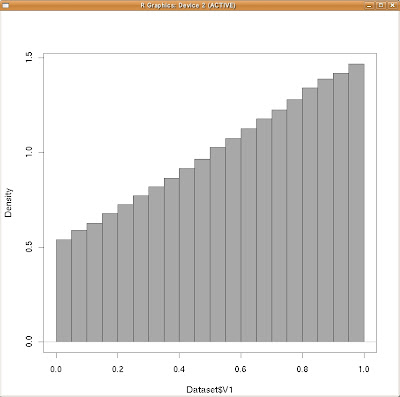    xの周辺分布(密度表示)



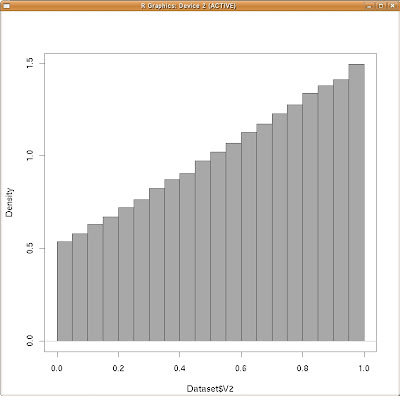    yの周辺分布(密度表示)


    これらも極限値の状態で滑らかになった場合、cqzypxさんが書かれた回答に近くなりそうだな、と言うことが分かります。特に切片辺りの値、そしてその最大値が大体一致しそうな事が分かりますね。

    こんなカンジで現代の統計学者も「良く分からない確率分布」「計算が大変そうな確率分布」を見かけた場合、ここで行ったようなメトロポリス法でそれらの確率分布に従う乱数を生成して、それらの性質を研究しているそうです。
    色々な確率分布に従う乱数を是非ともメトロポリス法で作成して、実験してみてください。


    R-Tips

    投稿者 cametan_001

    ラベル: , ,

    0 コメント:

    コメントを投稿