高校数学の窓LaTeX版: 質問＜３５６７＞２００７／６／２４from=みのる「合同式」

自然数ｍに対して
$5^{2^m}\equiv 1\pmod{2^{m+2}}$ 、 $\not\equiv 1\pmod{2^{m+3}}$
であることを、ｍに関する数学的帰納法で示せ。

1.の結果を利用して
$5^{2^{n-2}}\equiv 1\pmod{2^n}$ 　（ｎ≧２）、
$5^{2^{n-3}}\not\equiv 1\pmod{2^n}$ 　（ｎ≧３）
であることを示せ。

$5^{2^{m-1}}\equiv -1\pmod{2^n}$ 　（ｍ≧１）、
$5^{2^{m-1}}\not\equiv -1\pmod{2^n}$ 　（ｍ≧１、ｎ≧２）
を示せ。

ご教示願います。

うん、これもおかしな問題ですね。
もっと簡単に解けると思ってたんですが解けない。おかしいな、と思ってプログラム書いて調べてみたら、やっぱり題意が成り立ってないようです。
ちょっとここではDr.Schemeと言うフリーのプログラミング言語を利用して、問1が成り立っていない、ってのを調べてみましょう。問1が成り立ってなかったらそれこそ数学的帰納法的に(笑)、問2、問3も成り立つハズが無い、って事が分かるんで、労力省力化出来るでしょう。
Dr.SchemeのWebページは以下のようになっています。

右側にplatform:と言うプルダウンメニューがあるんで、ここで対応するOSのマシンを選びます。まあ、十中八九、Windowsマシンだとは思うんで、Windows (95 and up) x86でイイとは思うんですけどね。
ダウンロードが終わったら、デスクトップ上に次のアイコンが出来ているハズです。

このアイコンをダブルクリックすると、Dr.Schemeが起動します。画面写真は以下の様になっています。

2段に分かれたシンプルな画面構成ですが、基本的に、上段にはプログラムを書き込み、下段で実行します。上段をエディタ、下段をインタプリタと呼びましょう。
なお、ひょっとしたら、初回起動時、Choose Language(お好きな言語実装を選んで下さい)と問われるかもしれませんが、Pretty Bigを選んでおけばまあ、間違いないでしょう。
さて、Schemeと言うのもあまり聞きなれないプログラミング言語だとは思いますが、これはMIT(マサチューセッツ工科大学)では初級プログラミング言語として使われている由緒正しいプログラミング言語です。MITで初めてプログラムを学ぶ人はBasicより何より先にこのSchemeを学ぶようです。
んで、『何でこの問題で?』と言う理由ですが、もちろん、プログラミングが簡単だから、と言うのもあるんですが、このSchemeと言うプログラミング言語は再帰的定義を難なく使えると言う特徴があるからなんです。
この再帰的定義、って言うのはプログラミングの世界ですと『ちょっと難しい高尚な概念』と言う捉え方をされるケースが多いんですが、生憎、数学の世界では良く出てくる概念なんです。そうですね。数列とか数学的帰納法、ないしは漸化式なんかを直接書き下す事が出来るので、プログラミングを離れた数学の世界ですとかなり扱いやすいんです。通常、こう言う数列絡みをプログラミングする場合、ループ構文を使え、的な話をされる事が多いんですが、ループ構文自体をプログラムする方がメンド臭いのです。出来たら直接数式をプログラミング言語に翻訳して書き下せた方がイイ。そんなワケでここではSchemeを利用します。
まず問題としては $5^{2^m}\equiv 1\pmod{2^{m+2}}$ がどうなのか、だけをチェックしましょう。これが破綻している事さえ分かれば他の事はやらなくて済む。そこで、まずは左辺だけ、に着目してプログラミングをしてみましょう。平たく言うと $5^2$ のm乗を簡単に返してくれるプログラムを作ります。問題文ではmは自然数との事ですが、プログラミングの流儀に従って、 $m\ge 0$ とします。
取り合えず最初ですんで、次のプログラムを丸写ししてDr.Schemeの上段に書き込んで下さい。解説はアトに付けます。なお、;(セミコロン)のアトはコメントと言ってプログラム本体には何の関係も無い単なる解説です。

たった5行で $5^{2^m}$ を返すプログラムが出来ました。では内訳を見てみましょう。

Schemeのプログラムはカッコが大事。
Schemeと言うプログラミング言語はとにかくカッコだらけです(笑)。これは仕様なんでそう言うモンだ、って事で諦めて下さい(笑)。
ただし、Dr.Schemeのエディタではどのカッコとどのカッコが対応しているのか細かに教えてくれるんで、その点はあんまり問題無いでしょう(笑)。当然カッコの数が合わなければバグりますが、キチンと対応付けれる仕様になっているので問題無いとは思います。そして、全ての計算はカッコ内で行われます。そう言う仕組みなのです。
モノを名づける場合は(define 名前～で書き始める。
例えば、変数xに3を代入したい、と言う場合は
(define x 3)
とSchemeでは書きます。今は変数xの例ですが、別に関数でも何でも構わないのです。今回はsahenと名づけられた関数を書きたいので
(define sahen 関数の計算手順)
となっているのです。ここからその関数の計算手順を書き出します。
(註:なお、defineとは英語で定義しろ、の意。)
関数の計算手順は(lambda (引数)～で書き始める。
変数に数値を代入するのと違って、関数は計算手順を書かなければなりません。すなわち『ここから計算手順ですよ～』と言う何らかのサインが必要なんです。Schemeではそのサインとして
(lambda (引数)　具体的な計算手順)
と言う書き方を要求します。ここで引数とは、具体的にプログラムに外部から与えられる数の事を指します。この問題の場合、 $5^2$ のm乗を計算したいワケですから、mが外部から与えられる引数となり、結果
(lambda (m) 具体的な計算手順)
と言う構造となります。現時点で、全体的には
(define sahen (lambda (m) 具体的な計算手順))
と言う構造になっていますね。カッコが増えてきています(笑)!!!
(註:なお、lambdaとはギリシャ文字の $\lambda$ の事。どうして $\lambda$ なんだろ?と疑問が沸くでしょうが、そう言うモノだ、と思って下さい･笑。)

条件分岐の構造は(if (条件1)　結果1 (条件1以外の場合))と書く。

ここは数学の話、プログラムの話、半分半分です。まずは数学的帰納法に着目して欲しいんですが、大体このテの証明問題の場合、 $m=0$ ないしは $m=1$ の場合どう言う答えになるのか?そしてそのアト、一般の $m=k$ の場合どうなるのか尋ねます。つまり、最低でも条件は2つ、って事で尋ねられているんです。こう言うのを条件分岐と呼び、これをプログラム上で実現する手段がif構文と呼ばれるモノです。まあ、取り合えずそんなカンジで捉えていて下さい。ここで詰まってたら先に進みませんし、また、あとの項を読めば何やってるのか分かってくるでしょう。
ある数がゼロかどうか確かめるには(zero? ある数)で確かめる。
問題的にはmは自然数だ、との事ですが、別に左辺だけ計算する分には $m\ge 0$ で構いません。そこで、 $m=0$ の時に限って $5^{2^m}$ がどう言う値になるのか明示しないといけません。これが数学的帰納法の仕組みでしたね。そしてこの部分が、前項のif構文に関係ある部分で、最初の条件1にあたる部分なワケです。
(if (zero? m) 結果1 (条件1以外の場合))
と書き下せますね。
結果1には $5^{2^0}$ の計算結果を書き込む。
これは簡単でしょう。 $5^{2^0}=1$ ですよね?これをif構文に組み合わせて、4.、5.を鑑みると、
(if (zero? m) 1 (条件1以外の場合))
と書き下せます。そして日本語としてはmが0の時、計算結果として1を返せと読めますね。こう言うのを数学では初期条件等と呼んだりする場合があるようですが、プログラミング用語では脱出条件等と呼びます。つまり、m=0の時点でプログラムは計算を止める(脱出する)のです。では、最後のmが0以外の場合どう言う計算を行うのか、考えるのがこのプログラムsahenの最大の山場です。
Schemeの計算式は前置記法。
さて、本来だったら一番最初に書いておくべき事だったのかもしれませんが、最小の記述で最大の効果を上げる為にここに書く事になってしまいました。それはScheme独特の計算記述法の事に付いてです。通常、僕らが算数/数学で習う計算式の書き方は中置記法と呼ばれます。例えば、5に5をかけたい場合、×と言う記号を数字の間に挟んで5×5と表記します。ですから中置記法と言うんですね。一方、Schemeの場合は前置記法と呼んで、算術演算子は一番最初に置く、と言うような約束があるんです。同じく5に5をかけたい場合、
(* 5 5)
と表記するんです。ちょっと傍目には慣れない一風変わった書き方ではあるんですが、例えば $5^3$ を計算させたい場合、中置記法の場合5×5×5と×を二回書かないといけませんが、前置記法の場合、
(* 5 5 5)
と算術演算子を一回書くだけで事足ります。単純な差、と思うかもしれませんが、コード量が増えていくと、こんな単純な事でも随分と書く量が減ってありがたいんですよね。元々、コンピュータは人間の代わりにメンド臭い反復計算を行わせる為に開発されているので、逆に、人間が書く量はなるべく減らすに越した事が無いのです。じゃないと本末転倒です(笑)。
数列⇔再帰的定義の翻訳
さて、問題に戻って数学的帰納法で考えると、証明しなければならないのは、 $5^{2^m}$ のとき正しかったら $5^{2^{m+1}}$ のときも正しい、と言う明解なルールです。これが何で成り立つのか、と言うと、 $5^{2^m}=5^2\times 5^{2^{m-1}}$ が成り立ってるから、と言う背景があるから、ですよね。そこでプログラムでこの簡単な計算を実際書いてみます。問題は $m\not=0$ の時どうなのか、って事でした。Schemeの特色である前置記法に注意して書けば上で記述している $5^{2^m}$ の式は、
(* (* 5 5) $5^{2^{m-1}}$ )
と書けそうです(※)。こう言う風に書いていいのか?イイんですね、実は(笑)。忘れてるかもしれませんが(笑)、実は今作ってるsahenと言うプログラムは $5^{2^m}$ を計算するプログラムです。と言う事は $5^{2^{m-1}}$ を計算する為には今作ってるsahenと言うプログラムを呼び出し、(sahen (- m 1))を計算させればイイ、って事になります(プログラムsahenの引数はmですが、それよりも1つ少ない数を計算させる為に、引数が前置記法により(- m 1)になってる事に留意)。

『え?今プログラムを作ってる最中なのにその書いてる途中のプログラムを呼び出してイイの?』

って最初は大体ビックリするんですが(笑)、イイのです。これを再帰的定義と呼び、Schemeのお得意のワザなんです。そして、その方が、数学的帰納法/数列/漸化式関連でわざわざループ構文書いて････なんて方法より数学的にはスッキリしてるんですよね。なんせ数式そのままのプログラムへの翻訳ですんで。ぶっちゃけ、こう言う方法論は例えばMicrosoft Excelなんかの表計算プログラム上ではバグる方法論ですし(つまり再帰はサポートされていません)、他のプログラミング言語、例えばVBAなんかでは至極苦手な方法論なんです。通常は『再帰は避けろ』と言われる事が多いんですが、Schemeだったら殆ど問題無く再帰的プログラムを実行してくれます。それで今回数列を定義式通りに計算させる為にワザとSchemeを選んだのです。そしてそのお陰で何も考える必要が無いのです(笑)。

(※)実際は7.の前置記法に注意すれば、実は(* 5 5)をカッコで括って計算する必要が無く、
(* 5 5 (sahen (- m 1)))
とズラズラと書き連ねれば目的を達成できる事が分かるとは思う。ただし、ここでは問題文の $5^{2^m}$ を強調する為と初心者向け、と言う事で少々非効率的な書き方をした。

さて、プログラムsahenが完成致しました。以下はsahenを書き込んだDr.Schemeの画面写真です。

ここで一旦プログラムを保存しましょう。Dr.Scheme上部にSaveボタンがあります。

これをクリックするとエディタに書かれたプログラムを一旦保存してくれます。

Select a fileと言うポップアップが出てくるハズだと思うんですが･･････。まあ、取り合えず作ったプログラムに名前を付けましょう。そうですね・・・・・・ここではgoudoushikiと言うファイル名にしましょうか。ファイル名にgoudoushikiと打ち込みます。

[保存]ボタンを押してファイルをセーブします。
さて、今度は今作ったプログラムsahenを走らせてみましょう。まずは忘れないようにして欲しいんですが、プログラムを保存したら一旦Dr.Scheme上方にある[Run]ボタンを必ずクリックするようにして下さい。

では今度はプログラムsahenを下段のインタプリタ側にロードして実行します。インタプリタに以下のコードを書き込んで[Enter]キーを打って下さい。

(load "goudoushiki.scm")

これでファイルgoudoushikiはDr.Schemeに読み込まれます。なお、コレみても分かりますが、Schemeの場合、ファイルをロードするにしてもカッコが必要なんです(笑)。徹底してるでしょ(笑)?
なお、.scmってのは拡張子です。Schemeで記述されたプログラムは全て.scmと言う拡張子が自動的に付加されます。よって、ロードする場合、ファイルの性質を特定する為に必ず拡張子まで指定しなければなりません。
以上の作業が終了すると、以下の画面になるはずです。

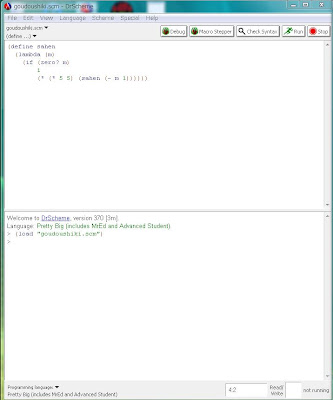
ちょっと実験してプログラムsahenが上手く動くかどうか試してみましょう。例えば $5^{2^2}$ を計算させたい場合、 $m=2$ なので、次のようにインタプリタに入力します。

(sahen 2)

そして[Enter]キーを打ちます。

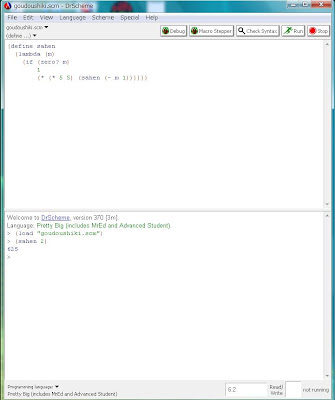
はい。確かに $5^{2^2}=625$ なんで上手く計算されているようですね。いくつかmを変えて検算してみて下さい。
次に右辺のmod内の式( $2^{m+2}$ )もプログラミングしてみましょう。プログラム名はuhenとしますが、今まで作ってきたファイル上に記述して構いません。今までの知識で十二分にプログラムは書けると思います(ないしはsahenをコピペして改造すれば作れるでしょう)。
注意すべきは脱出条件ですね。sahenは $m=0$ の時1を返しますが、uhenは $m=0$ の時何を返すべきか･･････?いずれにせよそんなに難しく無いと思います。ちょっと考えてみて下さい。

uhenも記述したDr.Schemeの画面写真は以下のようになります。ファイル名はgoudoushikiのままですんで、セーブは忘れないようにして下さい。

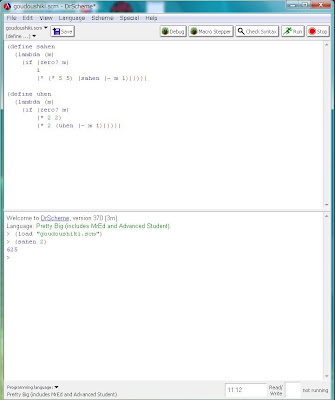
再びgoudoushiki.scmをインタプリタにロードして、uhenが返す数を検算してみて下さい。

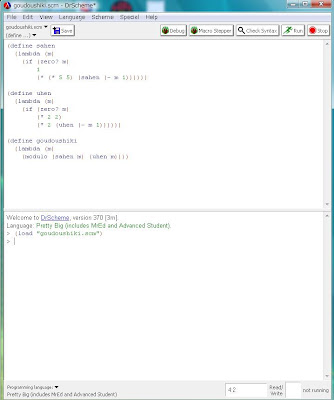
では、いよいよ3つ目のプログラム・・・・・果たして冒頭の命題が正しいのか正しくないのか、調べるプログラムを書こうと思います。しかもたった3行で済みます(笑)。今までで一番簡単なプログラムですよ(笑)。このプログラムをgoudoushikiと名づけて、次のように同じファイルgoudoushiki.scmに書き込みます。

はい。これだけです(笑)。
一行目、二行目は難しくないでしょう。今までのままです。
このプログラムの肝は3行目のmoduloと言う命令です。これは問題文にあるmodの事で、また、modと言うのもmoduloの略称です。すなわち、割り算での余りを返してくれる関数です。書式は以下のようになります。

(modulo a b)

このコマンドでaをbで割ったときの余りを返してくれます(これはインタプリタで実験してみて下さい)。
上のgoudoushikiのプログラムでは引数a、bの代わりに、最初に定義した二つのプログラム、sahenとuhenを引数mとして呼び出しています。その部分が

(modulo (sahen m) (uhen m))

と言う部分です。構文が(modulo a b)とまるっきり同じなのを確認して下さい。
また、これこそが、問題文にある、

$5^{2^m}?\equiv 1\pmod{2^{m+2}}$

かどうかを確かめる数式そのもののプログラムです。
さて、ここまで書いて、またgoudoushiki.scmをセーブします。そして[Run]ボタンを押して、またgoudoushiki.scmをロードしましょう。

では $m\ge 1$ に於いて、問題文の通り、 $5^{2^m}\equiv 1\pmod{2^{m+2}}$ なのかどうか調べてみましょう。 $1\le m\le 5$ くらいで調べてみれば充分なんじゃないですか?
次のようにインタプリタに入力してみて下さい。

(goudoushiki 1)
(goudoushiki 2)
(goudoushiki 3)
(goudoushiki 4)
(goudoushiki 5)

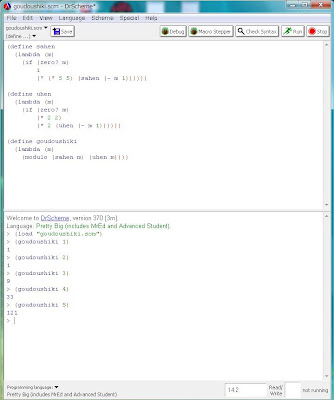
はい。ご覧の通りですね。m=3の時点で $5^{2^m}\equiv 1\pmod{2^{m+2}}$ と言う命題は破綻しています。 $5^{2^3}\equiv 9\pmod{2^5}$ なんです。
従って、この問題は数学的に破綻しています。解が無い、と言うのが結論になりますね。

以上です。

ここから余談です。
実は昨日、Googleの電卓機能を使って遊んでいたんですが、少々おかしな事に気づきました。
それは次の画面写真を見てもらえば分かります。

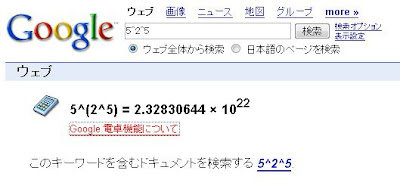
ん･･････?何･････?
$5^{2^5}$ は $(5^2)^5$ じゃなくって $5^{(2^5)}$ って計算すんの･･････?あら。知らんかった。
例えば、

$5^{(2^0)}\not=(5^2)^0$

ってのはすぐに分かります。あら、これは僕が勘違いしていたか･･････?
まあ、Google先生がそう言うのならそうかもしんない･･････。そう言う計算規則がある、って事は数学科卒の人には常識なのかもしんないけど、これは僕の無知の極みかしら?
そう思って、色々指数の計算法則の事に付いてググってはみたんです。ところが、そんなルールは特に明示されていないんですよね。つまり、通常は $5^{2^m}$ なんて曖昧な書き方はしないで、 $(5^2)^m$ とか $5^{(2^m)}$ とかキチンと書く、ってのが前提になってるんでしょう。そして、このテの計算が常識だったら、結構検索上位でヒットするハズなんですが、そう言うのは僕が調べた限り、特に見つからなかったのです。
なるほど。どうして、この問題が暫くの間ほったらかされていたのかが分かりました。他の数学が得意な回答者がレスを付けない、ってのはそれなりの理由があるんです。つまりあまりにも曖昧な問題なのです。どっちにせよ悪問なんでしょう。
ちなみに計算ソフト系では $5^2^m$ のように記入されたら $5^{(2^m)}$ として計算されるようです。ただし、調べた範囲内では、計算機で実行する上での約束事は、基本的にソフトの設計者が決める事ですから、数学的な計算の約束事と一致しているのかどうか、は定かではありません。後学の為に、この辺りの計算方法に明解なルールが存在しているのかどうか、ご存知の方は是非ともご一報を。

さて、Google先生の電卓の計算方法が成り立つ、とすれば数学的帰納法で証明しようがあります。ちょっとやっていってみましょう。

自然数mに対して $5^{(2^m)}\equiv 1\pmod{2^{m+2}},\not\equiv 1\pmod{2^{m+3}}$ であることを、mに関する数学的帰納法で示せ。
1. m=1の場合明らかに成り立つ。
  
  まあ、確かに $25\equiv 1\pmod{8},\not\equiv 1\pmod{16}$ になります。
  この時点で、 $25=2^4+2^3+1$ と書き換えられる事をアタマの片隅にでも置いておいて下さい。これが次からの手がかりになります。
2. m=kの場合 $5^{(2^k)}\equiv 1\pmod{2^{k+2}},\not\equiv 1\pmod{2^{k+3}}$ が成り立つとする。
  これにより、 $5^{(2^k)}=\alpha 2^{k+2}+\beta 2^{k+3}+1$ と書くことが出来ます。そして $\alpha$ 、 $\beta$ がどんな数なのかは問いませんが、題意を満たしているのは確認して下さい。つまり、 $2^{k+2}$ で $2^{k+3}$ は割り切れますが、逆は成り立たない、と言う事です。
3. m=k+1の場合
  
  最終的に $\gamma$ と $\delta$ がどんな数なのかは問いませんが、前出の $5^{(2^k)}=\alpha 2^{k+2}+\beta 2^{k+3}+1$ を利用して $5^{(2^{k+1})}=\gamma 2^{k+3}+\delta 2^{k+4}+1$ と言うカタチの式を導き出せば良い、と言う事です。
  ところで、 $5^{(2^{k+1})}=5^{(2^k \times 2)}=(5^{2k})^2$ と変形出来るので、
  
  $5^{(2^{k+1})}=(\alpha 2^{k+2}+\beta 2^{k+3}+1)^2$
  
  と書き表せます。展開すると、
  
  $5^{(2^{k+1})}$
  $=\alpha^2 2^{2(k+2)}+\alpha 2^{k+3}+\alpha\beta 2^{2(k+3)}+\beta 2^{k+4}+\beta^2 2^{2(k+3)}+1$
  
  となり、整理すると、
  
  $5^{(2^{k+1})}=(\alpha^2 2^{k+1}+\alpha+\alpha\beta 2^{k+3}+\beta^2 2^{k+3})2^{k+3}+\beta 2^{k+4}+1$
  
  となり、目論み通りの数式となりました。故に
  
  $5^{(2^{k+1})}\equiv 1\pmod{2^{k+3}},\not\equiv 1\pmod{2^{k+4}}$
  
  となり、題意は証明されたワケです。

1.の結果を利用して $5^{(2^{n-2})}\equiv 1\pmod{2^n}$ 　（ｎ≧２）、 $5^{(2^{n-3})}\not\equiv 1\pmod{2^n}$ 　（ｎ≧３）であることを示せ。

ネタ的には1.とほぼ同じです。
注意点としては下の関係が成り立っている、って事ですね。

n $5^{(2^{n-2})}$
$5^{(2^{n-3})}$
2 5 -
3 25 5
4 625 25
5 390625 625

つまり、当たり前なんですが、 $5^{(2^{n-3})}=5^{(2^{(n-1)-2})}$ の関係があり、 $5^{(2^{n-2})}=5^{(2^{(n+1)-3})}$ と言う事です。
従って題意は、

$5^{(2^{n-2})}\equiv 1\pmod{2^n},\not\equiv 1\pmod{2^{n+1}}$ (n≧2)であることを示せ。

ってのと丸っきり同じなんです。
つまり、n=m+2と置くと、証明の必要さえない、ってのがポイントとなります。n=2の時だけ、別立てで証明しておけばイイでしょう。

$5^{(2^{m-1})}\equiv -1\pmod{2^n}$ （ｍ≧１）、 $5^{(2^{m-1})}\not\equiv -1\pmod{2^n}$ 　（ｍ≧１、ｎ≧２）を示せ。

これも酷い問題だと思うんですけどね～～(笑)。この場合、nがどう言う範囲なのかからっきし分かりません。後者の方はまあイイんですが、前者でnはどんな値を取れると言うのか･･････?すくなくともn=0の時、題意はどの道成り立たないんで、多分前者はn=1の時に限り、と言う条件が自然に付加されそうな気もするんですが、いずれにせよ、それも単なる憶測なんで、この一連の問題は穴があり過ぎます。やらされる生徒の立場ではたまったもんじゃないですね。
まあ、いずれにせよ、

m≧1の範囲で $5^{(2^{m-1})}=2\alpha+\beta 2^n-1$ 、(n≧2)と記述できるかどうか調べよ

と言う問題に置き換えられるので、これを調べてみましょう。
1. m=1の時、 $5=2+2^2-1$ と記述できるのでこれは正しい。
2. m=kの時、 $5^{(2^{k-1})}=2\alpha+\beta 2^n-1$ と記述出来るとする。
3. m=k+1の時、
  $5^{(2^k)}=5^{2^{(k-1)+1}}=5^{(2\times 2^{k-1})}=(5^{2^{k-1}})^2$
  $=(2\alpha+\beta 2^n-1)^2$
  $=(2\alpha)^2-2^2\alpha+\alpha\beta2^{n+2}-2^{n+1}\beta+\beta^2 2^{2n}+1$
  $=(2\alpha)^2-2^2\alpha+\alpha\beta2^{n+2}-2^{n+1}\beta+\beta^2 2^{2n}+1+1-1$
  $=(2\alpha^2-2\alpha+1)2+(\alpha\beta 2^2-2\beta+\beta^2 2^n)2^n-1$
となり、題意を満たす事が分かります。

備考

Schemeで確かめてみる場合、さすがに $5^{(2^m)}$ がどうなるか、再帰で書くにしても骨が折れます(書けなくは無いのですが、名前付きletと言う局所変数のテクニックを使わなければならなく、そうなると数学の話と言うより一般的なプログラムの話になってしまいます)。
そこで指数関数を計算させる組み込み関数、(expt 底指数)と言うコマンドを使い、次のように記述します。

これで成り立つかどうか、試してみてください。
ただし、 $n=100$ 等と言う大きな数で計算してみると、さすがのSchemeでも止まってしまいます。と言うのも $5^{(2^m)}$ 等と言う計算はホント、数が大きくなり過ぎてオーバーフローしてしまうのです。ですから確かめるにせよ、 $1\le m\le 10$ 程度の範囲で止めておいて下さい。

2003年03月29日・数学「mod」・88点

高校数学の窓LaTeX版

高校数学の窓過去問検索

質問＜３５６７＞２００７／６／２４from=みのる「合同式」

Schemeのプログラムはカッコが大事。

モノを名づける場合は(define 名前～で書き始める。

関数の計算手順は(lambda (引数)～で書き始める。

条件分岐の構造は(if (条件1)　結果1 (条件1以外の場合))と書く。

ある数がゼロかどうか確かめるには(zero? ある数)で確かめる。

結果1には $5^{2^0}$ の計算結果を書き込む。

Schemeの計算式は前置記法。

数列⇔再帰的定義の翻訳

自然数mに対して $5^{(2^m)}\equiv 1\pmod{2^{m+2}},\not\equiv 1\pmod{2^{m+3}}$ であることを、mに関する数学的帰納法で示せ。

m=1の場合明らかに成り立つ。

m=kの場合 $5^{(2^k)}\equiv 1\pmod{2^{k+2}},\not\equiv 1\pmod{2^{k+3}}$ が成り立つとする。

m=k+1の場合

1.の結果を利用して $5^{(2^{n-2})}\equiv 1\pmod{2^n}$ 　（ｎ≧２）、 $5^{(2^{n-3})}\not\equiv 1\pmod{2^n}$ 　（ｎ≧３）であることを示せ。

$5^{(2^{m-1})}\equiv -1\pmod{2^n}$ （ｍ≧１）、 $5^{(2^{m-1})}\not\equiv -1\pmod{2^n}$ 　（ｍ≧１、ｎ≧２）を示せ。

備考

0 コメント:

New

分類

ツール

数学ガール

たけしのコマ大数学科

ガスコン研究所

数学系ブログ記事

n	$5^{(2^{n-2})}$	$5^{(2^{n-3})}$
2	5	-
3	25	5
4	625	25
5	390625	625