質問＜３５７７＞２００７／７／７from=にゃんこ「対数関数不等式の証明について」

、のとき
1.1＜＜1.2になることを証明せよ。

塾の講師をしている時に生徒に聞かれたのですが、
わたしは文系なので、全くわかりません。
よろしくお願いします。

---

ああそうですか(笑)。
僕の彼女も塾の講師のバイトしてたんで親近感覚えますね(笑)。
僕の彼女もバリバリの文系なんですが、数学教える事もたまにはあったようです。明○義塾では(笑)。
あそこは大学生のバイトをシフトで別教室にガンガン移動させる為、××専任ってのは難しいようで、しばしば専門外の事を教えなきゃいけないハメに陥るようです。ひょっとしたら同じ系列の塾かもしれませんね。○光義塾(笑)?

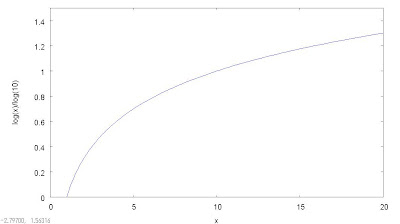
ってな与太はさておいて、文系なんで、って事なのでお聞きしますが、対数は分かりますか?多分一応高校で習ってるとは思うのですが･･････。数学のカリキュラムは結構変わるんで、属する世代が違うと共通認識ってのが結構持ちづらいんですよ。んで、取り合えず、対数とは何なのか、と言う説明は端折って、今回の議題に当たる10を底とした対数のグラフをお見せします。数字がどうのこうの、より先に『こう言うグラフの概形になるんだな』、と言う事を押さえておいて下さい。また、底が10の～と言う対数を特に常用対数と呼びます。従って以下のグラフは常用対数のグラフです。



まあ、こんな形をしているんですね。xの数値が増えれば増えるほど、の値も増えていくのが分かります。こう言うグラフを生み出す関数を特に単調増加型の関数と言います。
この単調増加、って概念が何の役に立つのか、イマイチピンと来ませんよね?ですが、次の事が言えるんです。

つまり、題意から言うと、取り合えずの方針としては近傍の数値が何であるのか、それと1.1、そして1.2の値との具体的な位置関係さえ掴めれば、取り合えず証明は終了だろう、と。そう言う方針は見えるワケです。
ところで、僕はインチキな人間なんで(笑)、こう言った問題を見ると、取り合えずは大体の状態を見る為に表計算ソフトなんかで実値求めてみちゃうんですね(笑)。具体的にの値を見てしまう(笑)。まあ、教わる側から言わせると、何を質問しても即刻何でも明解に回答してくれる先生なんてのは確かに頼もしいしカッコイイんですが、教える側としてはたまったモンではありません(笑)。なにぶん準備段階ってのが必要なんですよ(笑)。そんなに何でもかんでも期待されても、ねえ(笑)。
そこで、裏に回れば色々画策するワケです。生徒が見ていねえトコだったら何してたって構わんだろ、と(笑)。アンチョコ作るのも教育のウチ、なんですよ(笑)。あ、もっとも僕は全然教育関係無いですけどね(笑)。
さて、その表計算ソフトなんですが、一般では家計簿付けるのにしか役立たないソフトだと思われていますが、実は結構数学関数も豊富なんですよね。
一般に、表計算ソフトでは=log(数値)と言うコマンドで常用対数くらいは簡単に計算できます。ここではGoogle Docs & Spreadsheetsと言うオンライン表計算ソフトで作成したの範囲での常用対数表をお見せしたいと思います(もちろんMicrosoft Excelでも作成は可能です)。



こんなカンジになるんですね。
表計算ソフトの計算結果によると、辺りなそうなので、確かに題意であるってのは満たしていますね。ああ一安心(笑)。
とは言っても、表計算ソフトでそうだったから証明は終了ですとは参りません(笑)。個人的にはそれでもう充分だとは思うんですが(笑)、そうとはならないから数学ってヤヤコシイんですよね(笑)。
そこで。解が既に分かってる、と言う保険をかけた状態でどうやって題意を証明しようか、とここから知恵を絞るワケです。ここからが数学でしょうね。

対数計算の基本公式

さて、答えは既に分かってる、ってシチュエーションになっています。多分にインチキな状況なんですが、依然と問題状況としては

の具体的な値は分からない

と言う事にしましょう。見て見ないフリをする(笑)。
基本的な戦略としては、もっと手計算しやすいと思われる近傍の値、例えばであるとかそこら辺の値と1.1とか1.2とかの値と大小比較すればの値をどっかに閉じ込められるんじゃなかろうか、と言う方針です。そしてこの作戦が有効なのは常用対数の関数が単調増加、だからです。

え?だって計算出来ないでしょ?

とか思うかもしれませんが、そっちは案外ラクなんですよね。ただし、対数公式の知識が必要になります。これからそれらを紹介致します。

1. 


2. 


3. 


4. 


5. 


6. 

この6つが基本公式です。
んでぶっちゃけ『何でこうなるの?』なんてのは考えなくってイイです(笑)。ページ数も限られてますし、説明するのはメンドいです(笑)。『算数として』四則演算のつもりで暗記でもして下さい(笑)。意味が分からなくても計算は出来る、ってのが算数の強みです(笑)。
さて、そこで・・・そうですね。まずは大きい数から考えてみましょうか。ここでは近傍の数字として、まずはをピックアップしてみます。ピックアップの理由ですか?計算が簡単そう、だからです(笑)。公式の適用の練習代わりには丁度イイのではなかろうか、と。
まずは次の変換を試みてみます。

多分これは簡単ですよね。
さて、ここで上式に公式⑤を適用してみます。

そうすると、とは、の4倍の数と等価である、と言う事が分かるワケです。そして僕らはの値は初めから知っている。
従って、

となるワケです。残念ですね。1.2より若干大きかったようです。表計算の計算結果と照らし合わせてみてください。
では今度はもうちょっと小さい数値を狙ってみましょう。を計算対象にしてみます。
ここでは次のように分解出来ます。

今度は公式③を適用してみます。

なるほど。しかし僕らはが何なのか全然知りません。
こう言う場合はどうするのか・・・・・・しょーがないから作っちゃいましょうか(笑)。
は次のように記述できます。

そしてこれに公式④を適用します。

そして第1項に公式②を適用します。

これも上の表計算ソフトの計算結果と照らし合わせてみてください。
従って、は

になります。従って

なので、

より

だと言う事は分かりました。大きい方の数側の証明は以上で終了したワケです。
今度は小さい方の数を見てみましょう。狙う数はとしましょうか。
今までの知識ではすぐ計算出来るでしょう(練習です)。

･･････。困りましたね。は1.1より小さい。従っていまだに

の2つのパターンが存在するんですね。
気分はよろしくありません。以下のような気分です。


そこで・・・・そうですね。若干12より大きい数を持ってきてみましょうか。12より大きくて13より小さい数･･････12.5なんて良さそうですね。
ここで12.5ってのは25のです。すなわち対数で考えると次のような表記が可能です。

さて、これを計算してみると・・・・・・。

･････････。惜しいなあ。イイトコ行ってるんですけどね。再び次のような気持ちです。



んじゃあ、今度は12.5よりも大きくて、13より小さい数を探してみましょうか。
ここでは12.8と言う数を選んでみましょう。何故なら12.8は64のだから、です。そして64はと言う数だから、です。何で64なのか?と言うと、こう言う数はパソコンでプログラム書いてたりする経験ある人だとすぐ出てくる数なんですよね(笑)。ないしは麻雀の点棒計算得意な人、だとか(笑)。
いずれにせよ、対数表記をすると、

さて、上の計算を行うと、

となり題意を満たします。
すなわち、

と言う位置関係になっているワケです。

まあ、証明と言うほどエレガントでも無いのですが、ドラフトとしてはこんなカンジで充分でしょう。
あとは『証明』として、原稿を書き直して『私は初めっから全て分かってたんです』と言うカンジで生徒を煙に巻くのがコツだ、と言う事を申し添えておきます(笑)。悩んだ過程や試行錯誤は絶対に書いちゃいけません(笑)。威厳が損なわれます(笑)。

以上です。