質問<3708>2008年4月19日from=サル「統計学相対誤差」
2項分布の正規近似について
質問2997のエクセルでの回答を拝見させて頂きました。
同質問で構いませんが、標準正規分布Zを求め、
正規分布表を用いて相対誤差を求める方法を教えて下さい。
例の時で構いません。
、期待値
、
標準偏差、
かと思います。
宜しくお願いします。
★希望★完全解答★
一般に、二項分布
で近似出来る、と言われています。いわゆる標準正規分布ですよね。
ところで、上の式に例えば
と言うのも、確率密度はあくまで確率密度であって、確率ではない、ってのがミソなんです。
一般的に上式のような確率密度関数から確率を求めるには、ある値zが特定の微小区間内に存在するかどうか、を議論します。
具体的には確率密度と微小区間
上の式で始めて確率となるのです。
さて、まあ、これ以降は良く見かける議論ですが、一般に確率密度関数上の区間a〜b内に点zが存在する確率は
で書き表せます。まずここまでが準備段階ですね。
ここで上の式と目的とする二項分布
は離散分布である。
が取り得る数値は正の整数xであり、各xは当然ながら1づつ増加する。
- 一方、その性質は
では直接書き表せない。
- しかしながら特定の数値zが
の中に存在する確率は議論出来る。
この4つを考えてみると、多少インチキ臭いんですが、
を議論の対象とします。これなら区間a〜b内の長さは
従って、対象とする確率は
となります。
上の式は当然、
と書き換える事が出来ます。
さて、一般に、教科書の標準正規分布表では、上の
つまり、
または
の二つのどっちか、です。
両者とも左右対称である標準正規分布の右半分に付いての表なのは同じなんですが、計算して提示している数値が違います。手元の教科書でどっちの標準正規分布表なのか確認して下さい。なお、良心的な教科書だったら、前者の計算式に従った標準正規分布表は下側確率、後者の計算式に従った標準正規分布表は上側確率、と記載されている筈です。
下側確率の標準正規分布表の図形的意味 |
 |
上側確率の標準正規分布表の図形的意味 |
 |
※:ピンクの範囲の面積が確率の数値として標準正規分布表に記載されている。 |
いずれにせよ、二項分布
を下側確率の標準正規分布表から対応する値を探してきて計算するか、
を上側確率の標準正規分布表から対応する値を探して計算するか、だけです。
あとはご自分で頑張って計算してみてください。これ以降はメンド臭いですし(笑)、基本的に質問2997の作業と丸っきり変わりませんからね。
以上です。
以降は余談です。
自分で標準正規分布表を使って計算してみたら分かるでしょうが、
- それなりに誤差が大きい。
- 何より増して計算がメンド臭い。
ってのが分かると思います。
統計学はとにかく手計算には向きません。メンド臭すぎますね。
過去は、パソコンのパフォーマンスの問題があって大変だったのですが、現代はパソコンの能力が上がってきたんでそのテの問題は減ってきました。
ハッキリ言いますが、現代的な統計学の勉強法はパソコンでやった方がマシだ、と言う事です。分布表を用いた統計学の学習法は前時代的ですね。現代人とアウストラロピテクスくらいの差があります。
まあ、テスト前辺りに手計算をちょっとやってみる、ってのは悪くないですが、普段の勉強ではパソコン利用をお薦めします。そして理論の流れだけに集中して、それを良く理解する。
「そんな軟弱な!!!それは数学の学習法じゃない!!!」
と言う意見もあるでしょうが、大体理論がメンド臭い上に計算がメンド臭い、ってのは困りモノです。どっちか軽減する、としたら理論は省略出来ないので、計算の方なのは明らかです。パソコン利用してたって「何となく」理論を理解する事は可能ですし、「統計学」は実用に重きを置いているのが建前なので、使っているウチに「何となく分かってくる」分野です。しかも統計学は数学ではないので余計な心配をする必要はありません。
さて、以前はMicrosoft Excelが一番面倒がない、ってんで使ってたんですが、計算精度が色々な意味で若干不安なんで、統計解析ソフトRと言うフリーウェアを使った題意の計算法を提示しておこう、と思います。統計解析ソフトRの方が大規模データの解析にも比較的向きますし(なかなかそんなチャンスは日常生活上は無いのですが・笑)、将来的に統計学に関わるにせよ、使い方がある程度分かってたらツブシが効くでしょう。殆どの大学や研究所である意味「一番安価な(ソフト自体は無料ですが)」デファクト・スタンダードとなっているのが統計解析ソフトRなのです。
統計解析ソフトRのダウンロードとインストール
Rはタダで手に入るオープンソースの統計解析用ソフトウェアです。強力な統計関数とグラフィック関係のデバイスが含まれているので、この機会にダウンロード/インストールしてみましょう。
ダウンロード&インストールの方法:
- Windows 版 R のインストール
- Mac 版 R のインストール
- Linux 版 R のインストール
※:Rの最新版は2.7.0です(2008年4月24日現在)。
それぞれのOS用の指示に従ってダウンロード/インストール/初期設定を行ってください。
Rの起動
Windows版の場合はダウンロード/インストールが終わるとデスクトップ上にRのアイコンが出来てる筈なので、それをダブルクリックすればRが立ち上がります。

Linux版の場合は、まずは端末(ターミナル)を起動します。
コマンドプロンプトにただRと大文字で打ち込むだけでRが端末上で起動します。
Rに於ける確率分布の入力
Rでの二項分布と正規分布の確率を返すような入力は次の形で行います。
- 二項分布
dbinom(確率変数x, 試行数, 確率) - 正規分布
dnorm(確率変数x, 平均, 標準偏差)
Rで特徴的なのは、確率変数xは単一の値だけでなく、一種のベクトルとして数値を与えて、その解をまとめて返す事が出来る、部分です。
例えば、題意の様に0〜12までの13個の
dbinom(0:12, 12, 1/2)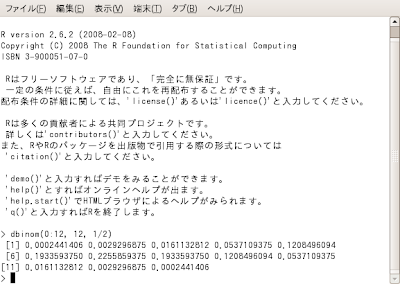
上の画面写真を見れば分かりますが、それぞれの確率変数xに対応した確率が一気に出力されます。確率変数xが複数ある場合、上のようにコロン(:)を使って
m:nの様な形で指定する事により、mからnまでの確率を複数一気に計算してくれるワケです。このように、コマンドラインでの操作は一見メンド臭そうに思うんですが、複雑な計算や大量の計算を行うには実はコマンドラインの方がメンド臭くないのです。マウスでコピペ、の方が大量のデータ操作の場合難儀になってくるんですね。
また、上のような計算結果を表示させるのではなく、何かに代入して保持しておく事が可能です。それは次のような形で行います。
B <- dbinom(0:12, 12, 1/2)Rでの代入は上記のように
<-を使って行い、=記号は用いません。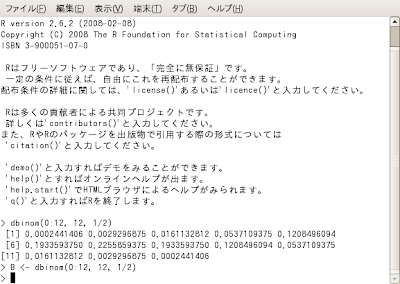
上のコードをRに入力すれば、画面写真を見れば分かる通り計算結果を返してくれません。
ただし、これは「計算結果をBに代入した」ワケで、B自体に結果は全て格納されています。
試しに、RでBと打ってみましょう。
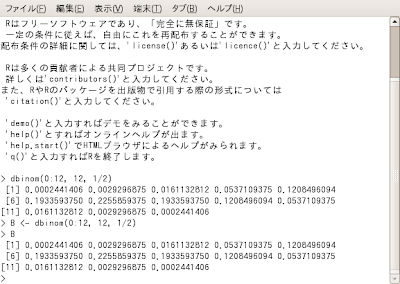
確かに計算結果が返ってきますね。
このように、一回計算した結果を何かに保存しておいていつでも結果を取り出せる、と言うのがRの強み、です。そしてその計算結果はパソコンのメモリが許す限り(そして貴方がそうしたがらない限り)、Rが閉じられるまで保持されます。
Rで作る統計計算スクリプト
以上でRの基本は終了です。ホントこれだけ、なんですね。
Rに搭載された全機能、特殊な統計関数の話をし出したらキリがないんですが、一方、Rの本質は「プログラミング言語」と言うよりは単なる「統計解析の為の道具」ですんで、基本操作系が複雑だったらお話にならないワケです。
つまり、プログラミング言語的な流儀ではなくって、単に計算の為のコマンドを羅列して行く事によってRでは各種の計算を一気に行うことが出来ます。そう言う「プログラムのようでプログラムではない」書き方を慣用でスクリプトと呼びます。Rで計算する指令はスクリプト程度で構わない、のです。
では、題意のスクリプトをちょっと書いてみましょう。
B <- dbinom(0:12, 12, 0.5) #二項分布を計算、保持
N <- dnorm(0:12, 6, sqrt(3)) #対応する正規分布を計算、保持
E <- (N-B)/abs(B) #相対誤差を定義に従い計算、保持
.Table <- data.frame(binom_dist=B, normal_dist=N, Relative_Error=E)
rownames(.Table) <- 0:12 #データフレームの1列目にラベルを作る
.Table #.Tableを表示
上のコードの1行目〜3行目は前項の「基本作業」そのままです。
注目すべきは3行目の
Eですが、これは計算式を見てみれば分かるように、相対誤差の定義に従って計算したモノをEに格納しているだけ、ですね。非常に電卓的な記述なのが分かると思います。ちなみにabsってのは想像通り絶対値を求める命令です。また、
(N-B)/abs(B)と言う計算式に含まれるNもBも前項で見たように、全て一種の行ベクトルとして出力されて複数の数値がある筈なんですが、Rではそれらの行ベクトルの要素を指定する必要は全く無く、全て対応する要素毎に先頭から順次まとめて計算して行ってくれます。そして計算結果のEも当然一種の行ベクトルに自然となっているのです。こう言う大まかな適当さ、ってのは通常のプログラミング言語では許されないんですが、一方Rはあくまで「統計解析の為に用いる」と言うのが前提で、「データを途中から読み出したりランダム指定する事は統計解析ではあり得ない」と言う割り切りで設計されているようです。つまり、Microsoft Excelで扱うような「表データ」相手に計算を実行するのが前提、となっているんです。
さて、4行目が問題なんですが、
data.frameと言う命令は引数に行ベクトルを複数取り、それらを列ベクトルに変換して格納するだけ、の命令です。まあ、そう考えて於いて間違いありません。書式は次のようになります。
data.frame(名前1=行ベクトル1, 名前2=行ベクトル2,...)
いわば、実は上のスクリプトに於いては
data.frameと言う命令は本質的には計算に何の関係も無い命令なのです。ただ、出力をMicrosoft Excelよろしくキレイに出力したい、ってだけの命令ですね。取りあえず今のトコそう言う「表計算型の出力を得る為だけの命令」って捉えておいて構いません。また、
(名前1=行ベクトル1, 名前2=行ベクトル2,...)と言う記述法で行ベクトルを引数として指定していくのですが、一方実は名前=ってのは省略しても構わない部分です。ただし、この形で指定しておくと、表計算型の出力にした時、列に「名前」が付くんです。つまり、上のスクリプトで、例えばbinom_dist=Bと言う指定で、B自体はそれ以前に計算した二項分布のデータなんですが、表示時に一番上にbinom_distと言う名前が表示されるだけの命令、ですね。そう言う意味なんです。あくまで「出力の見やすさ」の為に入れている、って事です。そして、上記の
data.frameを.tableに代入した後、先ほどと同様に
rownames(.Table) <- 0:12 も出力の一番左に「名前」を付ける為だけに存在します。これで0〜12まで出力してどの確率変数がどの確率に対応しているのか、見た目分かりやすくなりますね。
そして、最後に
.tableとして作った表を出力しているワケです。これを見たら分かる通り、先ほどのスクリプトで本質的な計算に必要な部分は全体の行の二分の一程度なんですね。あとは好みの問題ですが、出力表示を弄っているだけだったりします。
では上のスクリプトをRにでもコピペしてどうなるか見てみましょう。
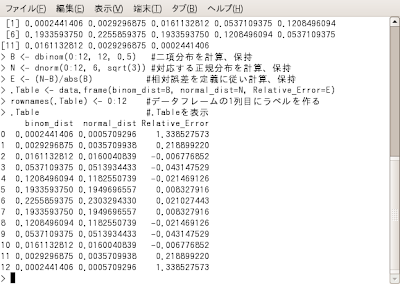
と言うワケでMicrosoft Excelまがいの出力表示が得られます。
Linux上でのTips
上の例では端末に直接コピペしましたし、実用上では殆ど問題が無いんですが、Linux等のオープンソースOSの場合、Windows等と違ってR用の独立したコンソール等は無いので、恐らくテキストエディタなんかを使って作業した方が効率は良いでしょう。
多分、Emacsなんかを使った方が便利だとは思います。
 | GNU Emacs恐らくUNIX系のオープンソースOSではもっとも有名でもっとも使われているテキストエディタ。 Emacs上で画面を二分割し、片方で端末を走らせる事で統合開発環境(IDE)としての役割も果たす。 当然、Rだけに限らず、様々なプログラミング言語で書かれるプログラムの媒体として使われる事が多い。 恐らく、Windowsも含め、世界でもっとも使用者が多いテキストエディタである。 |
Emacsは起動後、[Ctrl]+[x]キーを同時に押した後、[2]を押すと、画面が二分割されます。
 | Emacsの画面を上下2段に分割したトコロ。 Emacsでは、どんな作業でもこの2分割画面上で作業するのが基本。 |
そして、マウスでどっちかの画面の点滅カーソルを指定してから、[Alt]+[x]キーを押してshellと入力すれば、端末がEmacs上で起動します。
 | Emacs上で端末を起動したトコロ。 この例では下段を端末用にしている。 |
後は、端末上でRと打てば、Emacs上でRが起動します。
 | Emacsの下段でRが走ってる事が分かるだろう。 |
そして、上段をテキストエディタとしてR用のスクリプトを作成/編集/保存して、下の段で計算結果を見る、と言うのが作業の流れとなります(基本的にはSchemeなんかと変わりませんね)。
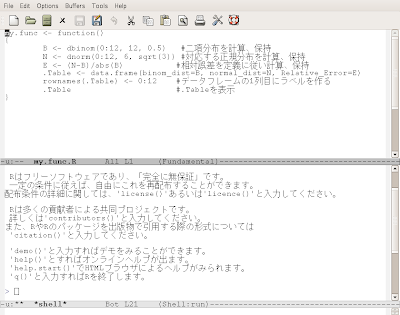
なお、EmacsでR用のスクリプトを作るにあたっての注意事項です。
- Rは汎用プログラミング言語程融通が利くようには作られていない。言い換えれば端末上で走らせるスクリプトを書けるくらい柔軟には設計されていないので、UNIX系OSでプログラムを書く時のような冒頭にシェバングなんかを記述しても無意味である。
- 前述の議論では単純なスクリプトを書いてRにコピペ、と言うやり方をしたが、テキストファイルにスクリプトをそのまま書いてRに読み込んでもそのまま実行してくれない。そう言う意味ではやはり汎用プログラミング言語と比べると融通が利かないのがRである。
従って、無引数の関数として
適当な関数名 <- function()
{
計算の為のスクリプト本体
}
としてスクリプト本体を包み込んでやれば良い。なお、関数名は本当に適当で構わない。上の画面写真ではmy.funcと言う適当な名前にしてある。 - 記述したスクリプトは".R"と言う拡張子を付けて保存する。上の画面写真ではmy.file.Rと言うファイル名で保存している。
- R側から作成したスクリプトを読み込むには
source("ファイル名")と拡張子込みで命令する。また、スクリプトファイル内に書かれた関数名を引数を付けて打てばR内で計算結果を表示してくれる。
特に4番に関してですが、例えばEmacsで作成したmy.func.Rと言うスクリプトファイルを保存した後、端末上のRで
source("my.func.R")
と打てば作成したスクリプトmy.func.RをRが読み込んでくれます。
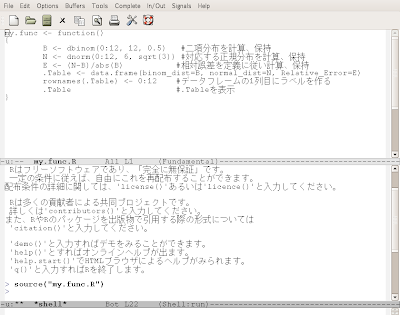
そして、スクリプトファイル内で記述された関数名を引数付きで呼び出せば、計算を実行してくれます。
my.func()
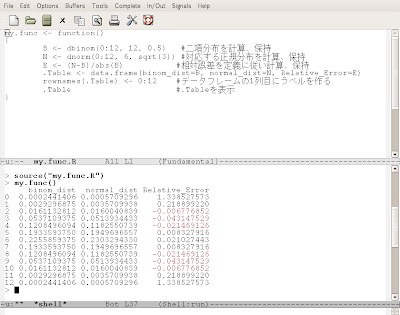
my.funcは無引数なんですが、括弧()自体は省略出来ない、と言う事に気をつけてください。もっとEmacsでRのスクリプトを簡易に編集出来るESS(Emacs Speaks Statistics)なるアドオンも存在するようですが、それに付いてはここでは扱いません。
詳しいESSの情報はコチラを参照して下さい。
Windows上でのTips
一方で、Windowsで行うRの操作の方が簡単です。
これはどっちがより良いシステムなのか一概には言えないんですが、Linuxと言うOSの設計思想とWindowsと言うOSの設計思想が根本的に違うトコに起因しています。それが同じアプリケーションでも操作性の差、として現れているんですね。
Linuxではコマンドラインの一貫性と編集環境の一貫性を追求している気があるので、その操作環境の構築さえ済めば殆どのソフトウェアを同一環境として使えるように設計されているワケです(例えばEmacsならEmacsだけで全ての作業が出来る、とか)。かつ、「押し付けの」環境があるワケではなくって「どの環境を選ぶのか?」個人の趣味に大きく委ねられています(当然Emacs以外にも色々な選択肢がある、って事です)。従って、実はその「環境設定」が若干メンド臭いんですが、一旦環境構築に成功してしまえば、あらゆるソフトウェア同士のデータのやり取り等が一環した環境の下で簡単にできるように設計されています。
一方、Windowsではそう言った「アプリケーション同士のデータのやり取り」に対する柔軟性がありません。アプリケーション類はアプリケーション類でそれぞれ「単体で存在する」ってのが基本です。その代わり、あるアプリケーション内での操作性の向上にはかなり力を入れられているんですね。具体的には直感的で分かりやすいインターフェースの採用、なんかが挙げられます。
実は本格的な統計解析を行う、なんて言った場合、WindowsはOSで使えるメモリの上限なんかが厳しく制限されているんで、最終的なRのパフォーマンスはLinux版等のUNIX系OSのヴァージョンには敵いません。が、「取っ掛かりの良さ」と言う意味ではWindows版に軍配が上がります。何せUNIX系は「環境の自由度」は大きいんですが、自由度が大きい故「何をどうしたらいいのか?」分かり辛いワケです。どう言うツールを探してどう設定するのか、初心者はそこで大きく躓く可能性が大きいのです。
OSとしての自由度が高い統一環境を追求するのか、アプリケーション毎の使いやすさを追求するのか、この設計哲学の相違はなかなか面白いモノがあります。
それはさておき、次がWindows版Rの画面写真です。
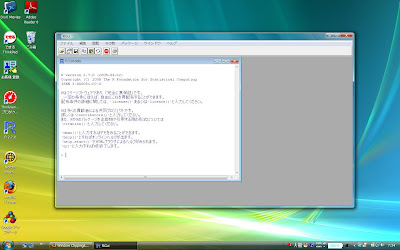
Windows版Rでスクリプトを書く場合は、[ファイル]プルダウンメニューから[新しいスクリプト]を選びます。
そうするとスクリプト記述用の[Rエディタ]が起動します。
[Rエディタ]にスクリプトを書き込みます。
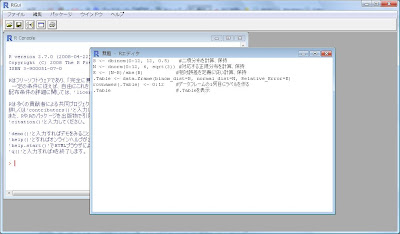
書いたスクリプトをマウスで選択した後、右クリックで[カーソル行または選択中のRコードを実行]を選びます。
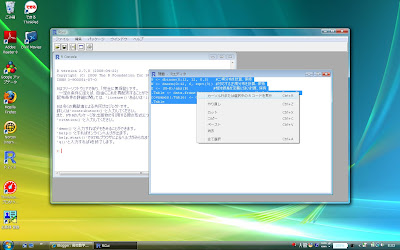
そうするとR Console側にスクリプトの計算結果が表示されます。
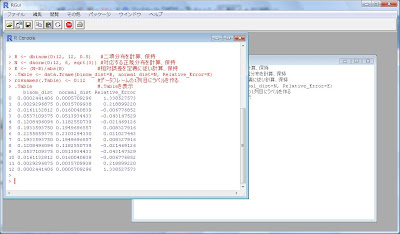
単なる計算スクリプトの実行だけだったらWindows版Rの方が保存も関数定義追加もしなくていいので簡単ですね。
こう言う簡易な方法でスクリプトを実行出来るのがWindows版Rの魅力です。
Rによる統計解析の基礎
Rによるデータ解析



0 コメント:
コメントを投稿