危険率の意味はなんとなくわかるのですが、今一計算に自信がありません。よろしくお願いします。
350人を無作為抽出して、飲酒と喫煙について調査。飲酒の程度の低い方からＡ１、Ａ２、Ａ３、
喫煙の程度の低い方からＢ１、Ｂ２、Ｂ３、Ｂ４と分ける。結果は表1を示した。
飲酒と喫煙は関係があるか、危険率５％で検定せよ。
（表１）
| | Ｂ１ | Ｂ２ | Ｂ３ | Ｂ４ | 計 |
| Ａ１ | 39 | 54 | 49 | 17 | 159 |
| Ａ２ | 27 | 43 | 40 | 9 | 119 |
| Ａ３ | 14 | 23 | 15 | 20 | 72 |
| 計 | 80 | 120 | 104 | 46 | 350 |
よろしくお願いします。
★希望★完全解答★
危険率の意味はなんとなくわかるのですが、今一計算に自信がありません。
さ〜て……困りましたねえ。
ぶっちゃけた話、危険率の意味が分かろうと分かるまいと構わないんですが、いくつか不明瞭な点があります。
例えばこの問題を見たとき、
どの検定を行うべきか分かりますか?
危険率がどうだろうと、そっちの方が大事なんです。まずそれがサルさんの質問を見る限り分かんないんですよ。
んで
今一計算に自信がありませんとの事ですが、それも別に構わないのです。
どの道、人間である以上、計算間違いは起こるモンなんで別にそれは責められる筋合いの話ではないです。
大体、
前回言った通り、正確な計算を試してみたければこれはパソコンに頼れば一発解決です(この方法は後述します)。
従ってわざわざここで答え合わせをする必要は無いんです。
余談なんですが、最近気づいたんですけど、某通信教育制大学のレポート課題が
高校数学の窓に多数投稿されているんですね。別にそれ自体は悪い話じゃないんですが、明らかに回答をそのまま丸写ししてレポートとして提出したい、って思ってる人もいるらしく、これはあまり芳しい傾向じゃないです(そう言う人は本来だったら有料の
HAPPYCAMPUSでも使うべきでしょう)。大体それじゃあ「レポート課題」の意味が無いですし、かつ、ネットで検索したら「解答まるまる載ってた」って状況は避けた方が良いんじゃないか、と言う風に最近は警戒しているのです。
別にサルさんがその「某通信教育制大学の学生だ」って言ってるワケじゃあないんですが、一応、「どこまでやってどこから分からなかったのか」差別化の意味でも書くようにした方が良い気がします。じゃないとこちら側もどこがツボか分からないのです。
で、問題の検定ですが、これは
検定、と言われるモノを使います。
が、確かに、通常、統計学の教科書では
検定辺りになってくると天下りに公式を適用しろ、ってニュアンスになってくるのも事実で(確かに説明がメンドっちい・笑)、よってここでは一応、亀田自身が「理屈のツボ」だと思っている部分だけ解説しておきます。
そうすれば「どうしてそう言う処理をするのか?」ちょっとは分かるでしょう。そこさえ分かったら後はパソコン任せでも構わないのです。
確率変数の独立性の意味を把握する
質問＜3582＞でも書きましたが、基本的に確率が独立であるとは、
を指します。と言うかこれが独立の定義です。
何故ここで確率変数の独立性なんてワケの分からないモノが出てくるのか?
それは数理統計の世界では独立じゃなかったら関係してる、と言う単純な二律背反があるからです。
これはピンと来ないかもしれません。例えば僕と長澤まさみちゃんが「独立じゃなかったら関係している」とは現実では断定出来ないのは大変残念なんですが(笑)、一方、数理統計の分野では大胆に「独立じゃなかったら関係している」と言う単純な仮定を置いてるからです。問題は検定、と言う文脈では「どのくらい関係しているのか?」と言う定量的な判断を下さない、と言うトコに秘密があるのです。
ちなみに僕は別に長澤まさみちゃんのファンでも何でも無いんですけどね。あれ?何の話してたんだっけ(笑)?
あ、そうそう、次の例をちょっと見てみましょう。例えば、問題の表が次のような「中間部に何も記入されていないまっさらな状態」だったとします。
| | Ｂ１ | Ｂ２ | Ｂ３ | Ｂ４ | 計 |
| Ａ１ |
|
|
|
| 159 |
| Ａ２ |
|
|
|
| 119 |
| Ａ３ |
|
|
|
| 72 |
| 計 | 80 | 120 | 104 | 46 | 350 |
さて、ここで上の表の升目を確率ですべて埋めなさいと言う問題があったとします。出来ますか?出来ませんよね。何故なら色々なパターンがあり得るから、です。ただしAと言う事象とBと言う事象が独立だったとすると言う条件さえあればこれは解けるんです。
例えば、A1とB1が交差する升目の確率を
として、事象A1とB1が丸っきり関係ないとしたら、
と独立の定義に従って計算が可能です。
さて、計算に使う
と
ですが、これは表から求められますね。
| | Ｂ１ | Ｂ２ | Ｂ３ | Ｂ４ | 計 |
| Ａ１ |
|
|
|
| 159 |
| Ａ２ |
|
|
|
| 119 |
| Ａ３ |
|
|
|
| 72 |
| 計 | 80 | 120 | 104 | 46 | 350 |
つまり、とが互いに全く関係ないとしたら、これらは上の赤枠に記述された数値を利用して
に成らざるを得ないのが分かるでしょう(ここは非常に小学生的な計算です)。
従ってとが互いに関係が無ければ
となり、結果表のA1とB1が交差する場所は次のように埋める事が出来ます。
| | Ｂ１ | Ｂ２ | Ｂ３ | Ｂ４ | 計 |
| Ａ１ |  |
|
|
| 159 |
| Ａ２ |
|
|
|
| 119 |
| Ａ３ |
|
|
|
| 72 |
| 計 | 80 | 120 | 104 | 46 | 350 |
つまり、A1とB1が互いに関係していたとしたら升目が取る確率は上の理論値から乖離していく筈だと言うのが第1に押さえるべきポイントとなるんです。
比較しやすいように変換する
上の計算を各升目に適用すると、理論上でのAとBが独立だった場合の確率が各升目毎に求まります。
が。しかしながら。元々の表で与えられた升目には確率が記入されているワケではありません。あくまで単位は人数ですよね。
そこで、先に求められた理論的な確率を用いて各升目を埋めるべき理論的な人数を求めます。これは簡単ですよね。
これが期待度数等と呼ばれているもので、恐らく殆どの統計の教科書では次の式がいきなり天下りに書かれている筈なんです。
変数Aの第iカテゴリー，変数Bの第jカテゴリーの期待度数
は、第i行の合計を
、第j列の合計を
、総数をnとして
で表される。
ただし、これは先ほど見た通り、元々は
の事で、従って、
と言う計算結果として出てきたモノなんです。そこを押さえておいてください。
ピアソンの適合度基準を計算する
上の理屈の背景まで分かれば後は天下りです。実測された升目毎の人数を
とすると、実測値と理論的な期待度数の乖離具合を調べる為の指標、ピアソンの適合度基準と呼ばれる数値は
で算出されます。
これも上の式は見た目厳めしいんですが、指示している内容は小学校の算数レベルです。統計ってのは数式がややこしいように見えることは見えて、実際問題、計算自体も確かにメンド臭いんですが、一方、行うべき計算は実は小学校の算数レベルの事が多いのです。
例えばA1とB1が交差している升目は
- 実測値は問題にあるように39である。
- 理論上の期待度数は2.の計算を実行すると
である。
- 従って、(何て呼べば良いのか分からないが)A1とB1が交差している升目に対応しているある数は
であり、これを計算する。
- 同様の計算を他の各升目全部に対して行う。
- 結果をすべて足せばピアソンの適合度基準になる。
と言うように、実は指示している計算は単純かつ単調な内容なのです。実際この計算を行うとなるとメンド臭いだけ、って事ですね。内容自体は大した事言ってません。
さて、この計算で求まるピアソンの適合度基準は要するに値の事で、この値は当然分布での確率変数です。
後は、普通の検定と作業は同じですね(もちろんここが分からなかったらお話になりませんが)。分布の表を使って対応する確率を探し……と言うような作業になるんですが、メンド臭いんで、すべてパソコンで行います。統計解析ソフトRの出番です。
統計解析ソフトRのダウンロードとインストール
Rはタダで手に入るオープンソースの統計解析用ソフトウェアです。強力な統計関数とグラフィック関係のデバイスが含まれているので、この機会にダウンロード/インストールしてみましょう。
ダウンロード&インストールの方法:
※:Rの最新版は2.7.0です(2008年4月24日現在)。
それぞれのOS用の指示に従ってダウンロード/インストール/初期設定を行ってください。
Rの起動
Windows版の場合はダウンロード/インストールが終わるとデスクトップ上に
Rのアイコンが出来てる筈なので、それをダブルクリックすれば
Rが立ち上がります。
Linux版の場合は、まずは端末(ターミナル)を起動します。
コマンドプロンプトにただ
Rと大文字で打ち込むだけで
Rが端末上で起動します。
パッケージのインストール
Rの優秀なトコロは、数々の特殊な機能をまとめたプログラム群を追加インストール可能である、と言う部分です。これを
パッケージと呼びます。
今回利用するパッケージは
Rcmdrと言うパッケージです。
Rcmdrと言うパッケージはコマンドラインバリバリの
Rにマウス操作の為のGUI環境を加える為のモノでこれは結構重宝します。詳しくは
このPDFに書いてあるので、参考にして下さい。マウスだけで基本的な
Rの操作が出来るようになります。
Windows版
Rでのパッケージのインストール方法は、RGui上部にある[パッケージ]プルダウンメニューから[パッケージのインストール...]を選びます。
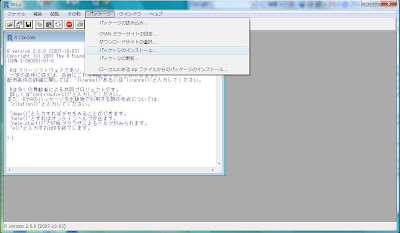
そうしたら、「どこのミラーサイトからダウンロードするのか?」尋ねてくる[CRAN mirror]ポップアップが出て来ます。
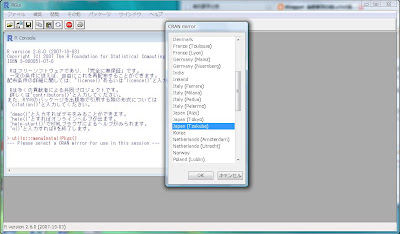
現時点では日本の
Rのダウンロード先は
の3箇所となっています。近場の大学のサイトをクリックして[OK]ボタンを押しましょう。
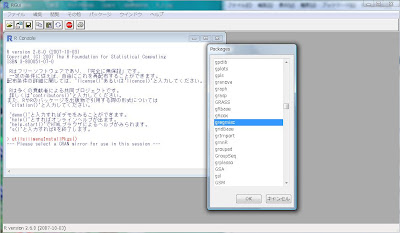
そうすると、インストール可能なパッケージのリスト、[Packages]ポップアップが出てきます。スクロールして、目的のパッケージを探し出してクリック、そして[OK]ボタンを押してください。
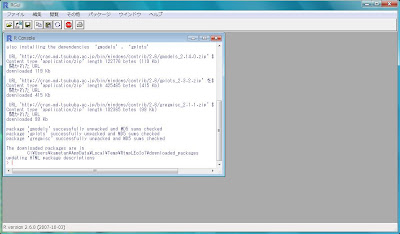
無事パッケージのダウンロードが終わります。
Linux版
Rでのパッケージのインストール方法は、端末(ターミナル)で次のようなコマンドを入力します。
install.packages("ダウンロードしたいパッケージ")
例えば、今回Rcmdrが必要なワケですから、次のように端末のコマンドプロンプトに入力します。
install.packages("Rcmdr")
すると、R上で次のようにパッケージのダウンロードが始まります。
註:Ubuntu/Kubuntuの場合は、R経由でインストールするより、Synapticパッケージ・マネージャないしはAdeptパッケージ・マネージャ経由でインストールした方が確実かもしれません。
Rcmdrの起動方法
Rcmdr(Rコマンダー)はWindows版では、まずはRGui上部にある[パッケージ]プルダウンメニューから[パッケージの読み込み...]を選びます。
そうすると[1つを選択してください]ポップアップが出てきますので、パッケージの一覧から[Rcmdr]を探し出してクリックして[OK]ボタンを押します。
それにより、Rコマンダーが以下のように起動します。
以降は、基本的に亀田はLinuxユーザーなので、Linux版の画面写真を元に解説していきますが、Rコマンダー及び
RはLinux版でもWindows版でも全く同じように操作出来るので、ご心配は無用です。
Rcmdr(Rコマンダー)はLinux版では、コマンドラインで起動します。
端末(ターミナル)で次のように打って、Rcmdrを起動します。
library(Rcmdr)
そうするとRコマンダーが起動します。
これを使えば基本的な
Rの操作を全てマウスで行う事が出来ます。
Rでのカイ二乗検定
前回はコマンドラインで
Rを操作しましたが、今回はGUIでやります。まあ、その方がメンド臭くないでしょう(ケースバイケースです)。
|
Rコマンダーの[統計量]プルダウンメニューから[分割表]→[2元表の入力と分析...]を選ぶ。
|
|
[2元表を入力]ポップアップメニューが表れる。
|
|
- 行数:問題に合わせて3にします。
- 列数:問題に合わせて4にします。
数を入力:問題に従って表の数値を入力します。
パーセントの計算:弄らなくて結構です。
仮説検定:[独立性のカイ2乗検定]を選びます。
すべての設定が終わったら[OK]ボタンを押します。
|
|
計算結果が表示されます。
|
さて、結果の見方です。
Pearson's Chi-squared test
data: .Table
X-squared = 18.6655, df = 6, p-value = 0.004767
これは日本語に直すと次のような意味です。
ピアソンのカイ二乗検定
データ: .Table
カイ二乗値 = 18.6655, 自由度 = 6, p-値 = 0.004767
まあ、検定の名前はいいですね。そのまま
カイ二乗検定(Chi-squared test)ですんで。
さて、先ほど手計算が大変だ、と言った
ピアソンの適合度基準がRコマンダーでの出力である
カイ二乗値(X-squared)です。質問にある
今一計算に自信がありませんと言う部分は、取りあえずこの値を比較して下さい。ここで計算間違いしてれば当然答えが違う、と言う事です。
自由度(df=degree of freedom)はいいですね。
分布は
自由度によって形が変わりますし、と言うことは適切な自由度の
分布表の値を参照しないとおかしな結論になります。そして、自由度の計算方法に付いては
教科書に書いてある筈です。今回の表だと自由度は6です。何故6になるのか、教科書と見比べて計算してみてください(大した計算じゃない筈です)。
問題は
P値ですね(他に
有意確率とも呼ぶ)。これは古い数表を使ったタイプの統計学の教科書では出てこない概念です。とは言っても実は簡単な内容で、これは単にこの例の場合のデータから計算した
値に対応した
分布の端っこの確率です。問題の要請によると、このP値が5％より大きければ検定は失敗、小さければ成功、です。0.004767ってのは5％よりも小さいので検定は成功です(と言う事は結論はどうなるでしょう?考えてみてください)。
数表を使う場合は、問題の要請(危険率)から逆に対応する
値(パーセント点)を探しだし、それとデータから計算した
値の大小比較をするんですが、現代のコンピュータ利用による検定では直接確率同士を比較する方法論に変わってきています(こっちの方がやり方は新しいのです)。
|
自由度6の分布の図。
右側のピンクに塗られた面積が全体の5％の面積を占める。
計算した値がピンクの範囲内に入ってるのかどうか調べる、のが検定作業の図形的な解釈。
また、分布だろうと何だろうと、確率分布としての大まかな性質は全く同じで、要するに確率密度が大きい確率変数は出易く、確率密度が小さい確率変数は出にくいのである。具体的には、確率分布の端っこの確率変数は出づらい、と言う事だ。逆に言うと、左の図では値が5付近だったら一番出易いのである。
これは、例えばコインの表が出る確率が1/2と仮定した場合、10回のコイントスで10回が10回とも表が出ると言う事は殆どあり得ない、と言うのと同様である。つまり、こう言う結果が出たらコインの表が出る確率が1/2だと言う仮定を疑った方がマシだ、と言うのは誰でも分かるだろう。これが統計的仮説検定のカラクリであり、それが帰無仮説の棄却、と言う意味である。
|
以上です。
統計解析フリーソフトR入門[GUI版R]R Commander
独立性の検定
や
辺りでも取り上げられていたテクニックです。
投稿
